I am assuming that we are talking about 2 different systems since x=y in the first and x=y in the second For the first system where x = y, simply substitute x for y Then 6x 2y becomes 6x 2x Please answer these using both substitution method and elimination method 8439 Azraelle26 Junior High School answered Please answer these using both substitution method and elimination method 2xy= 18 y=x10 3xy= 7 2x3y= 10 x2y= 18 y= 2x16 2xy=12 x=y15 xy=12 2xy=17 2 See answers Advertisement Advertisement Kafkaesque answers Solve the system of equations using Substitution method 1 2x 3y = 11 x = 2y 2 2 2x 3y = 2 y = 2x 10 3 3x = 18 x = 2y 16 4 2x 4y = 2 x 2y = 1 5 3x 4y = 1 x 12 = y
3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall
3x y=10 x-y=2 substitution method
3x y=10 x-y=2 substitution method- 🔴 Answer 1 🔴 on a question Use the substitution method to solve the system of equations choose the correct ordered pair 3xy=10y=x2 the answers to answerhelpercom Ex 34 , 1 (Elimination)Solve the following pair of linear equations by the elimination method and the substitution method (ii) 3x 4y = 10 and 2x – 2y = 2 3x 4y = 10 2x – 2y = 2 We multiply equation (2) by 2 2(2x – 2y) = 2 × 2 4x – 4y = 4 Using elim




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
solvingequations systemofequations functions math slopeinterceptform physics homeworkhelp trigonometricidentities integration substitutionmethod limits calculus 13,435 questions 17,804 answers Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (iii) 3x – y = 3 9x – 3y = 9 3x – y = 3 9x – 3y = 9 Solving (1) 3x – y = 3 3x = y 3 x = (𝒚 𝟑)/𝟑 Putting value of x in (2) 9x – 3y = 9 9((𝑦 3)/3)−3𝑦=9 3(y 3) – 3y = 9 3y 9 – 3y = 9 3y – 3y 9 = 9 0 9 = 9 9 = 9 The statement is true for all values of x So If the linear equation in two variables 2x –y = 2, 3y –4x = 2and px–3y = 2are concurrent, then find the value of p If ܽa b = 35 and a − b =
use the expression for y from the first equation in the second equation then the equation y = 2 x 6 becomes 3 x 10 = 2 x 6 add 3 x to both sides 10 = 3 x 2 x 6 10 = x 6 subtract 6 from both sides x = 4 Now replace x with 4 in the first equation to find yAre solved by group of students and teacher of Class 10, which is also the largest student community of Class 10 x=4 and y=1 Stepbystep explanation xy=3(1) x=3y 3x2y=10 (2) putting the value of x=3y in equation(2) we get, 3(3y)2y =10 93y 2y = 10 y =109=1 putting the value of y=1 in equation (1) we get x1=3 x=31=4 Thus the value of x=4 and y=1 is found by substitution method
Solve the following system of equations by using the method of substitution 2x3y=9,quad 3x4y=5 Apart from being the largest Class 10 community, EduRev has the largest solved Question bank for Class 10 Upgrade to Infinity This discussion on Solve using substitution method 3x/25y/3=2 , x/2 y/2=13/6?ans x=2,y=3?Othersiwe, the solution may have a complex meaning when dealing with systems of higher orderCommon examples include simultaneous equations with squares eg y^2x^2=2;xy=1 For a step by step solution for of any system of equations, nothing makes your life easier than using our online algebra calculator




For A Pair Of Equations 2x 3y 10 And 3x Y 4 Find X




Tim Kerins Leaving Certificate Honours Maths Algebra Tim Kerins The Date Pdf Free Download
Question 3093 1Use the Substitution method to solve the system of equations x y = 10 y = x 8 2Use the Substitution method to solve the system of equations 3x y = 5 4x 7y = 10 3Use the Substitution method to solve the system of equations y 2x = 5 3y x = 5 can you please help me solve each step by step so i can under stand9x9y=9 > 3x3y = 3 > 3x = 3y3 3x13=ySub for 3x into the 2nd eqn 3y3 13 = y 3y10 = y 2y = 10 y = 5 x = 6The only ordered pair of the solution is (6,5)PS Most people would have subbed for y into the 1st eqn, but that's not the only way to do itIf you substitute the values x= −5 and y= 2 into the second equation, you get a false statement 2(2) − 10 = 2(−5) To solve this system, try rewriting the first equation as x= 2y− 8 Then substitute 2y− 8 in for xin the second equation, and solve for y The correct answer is x= −2, y= 3 D) x= 0, y=




Solve The Simultaneous Equations 10 X Y 2 X Y 4 15 X Y 5 X Y 2




Solve By Substitution Method 3x 5y 1 And 2x Y 3 Scholr
2x4y = 104x5y = 26 None of the coefficients are 1 So we can choose to make any variable the subject Lets make x the subject of Equation 1 x = (10 4y)/2 x = 5 2y Next, substitute this expression for x in Equation 2 andAlgebra questions and answers Question 5, 4141 Score Points Solve the given system by the substitution method 3x y = 17 4x 2y = 6 Select the correct choice below and, if necessary, fill in the answer box to complete your choice O A The solution is (Type an ordered pair) OB There are infinitely many solutions, O C There is no solutionSolve by the substitution method and then two ordered pairs!



What Is The Value Of X And Y If Xy 10 And X Y 3 Quora




Solved 6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com
3x y = 2 Y = 3x 2 (1) 2x y = 8 2x (3x 2) = 8 2x 3x 2 = 8 5x = 5x = 10 X = 10/5 X= 2 Now putting rhe values in (1) Y = 3(2) 2 Y= 62 Y= 4 The Questions and Answers of Solve these linear equations by substitution method 3x/2 5y/3 =2 x/3 y/2 =13/6?Finite Math Solve by Substitution x2y=10 , 2xy=10 , x2y=10 x − 2y = −10 x 2 y = 10 , 2x y = 10 2 x y = 10 , x 2y = −10 x 2 y = 10 Add 2y 2 y to both sides of the equation x = −10 2y x = 10 2 y 2xy = 10 2 x y = 10 x2y = −10 x 2 y = 10 Replace all occurrences of x x with −102y 10 2 y in each




X Y 3 And 3x 2y 10 By Substitution Method Maths Pair Of Linear Equations In Two Variables Meritnation Com
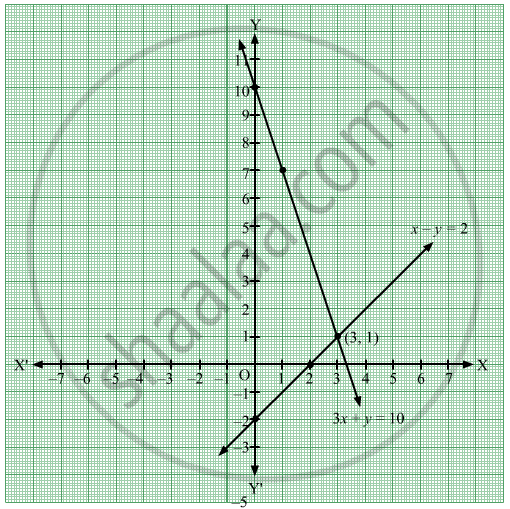



Solve The Following Simultaneous Equation Graphically 3x Y 10 X Y 2 Algebra Shaalaa Com
NCERT Solutions for Class 10 Maths Chapter 3 Exercise 34 Question 1 Summary On solving the pair of equations by the elimination method and the substitution method we get x, y as (i) x y = 5 and 2x 3y = 4 where, x = 19/5, y = 6/5 , (ii) 3x 4y = 10 and 2x 2y = 2 where, x = 2, y = 1 , (iii) 3x 5y 4 = 0 and 9x = 2y 7 where, x = 9/13, y = 5/13, (iv) x/2 2y/3 = 1 and x y/3 Substitution method worksheet pdf 2 substitute the expression into the other equation and solve for the variable 1 y 3x 5 4x 7y 19 6 y 6x 11 y x 9 2y 4x 14 7 2x 8y 6 8 x 2y 1 y 7 x 3x 2y 3 Steps 1 solve one of the equations for x or y Integration worksheet substitution method solutions a let u 4x 5 b then du 4 dxor 1 4 du dx c now substitute z p 4x 5 dx z u 1 4 du z 1 4 u1 2 du 1 4 u3 2 What is the Substitution Method?




Ex 3 6 1 Vii And Viii Class 10 Ncert Solutions Maths



What Is The Value Of X Y If X Y 10 X Y 15 Quora
Use the Substitution method to solve the system of equations 3x4y=10 y=x1 Answers 2 Get Other questions on the subject Mathematics Mathematics, , mairadua14 To decrease an amount by 16% what single multiplier would you use Answers 1You want to get one variable all by itself on one side of the equation x 2y = 10 2y x = 10 2y Now, substitute that value for x into the other equation 3(10 2y) y = 2 Solve for y y=4 Now, sub that value back into x = 10 2y x = 10 2(4) Solve x = 2(x, y) = (2, 3) Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here If you have any feedback about our math content, please mail us




Solved Exercises Use The Substitution Method To Solve Each Chegg Com
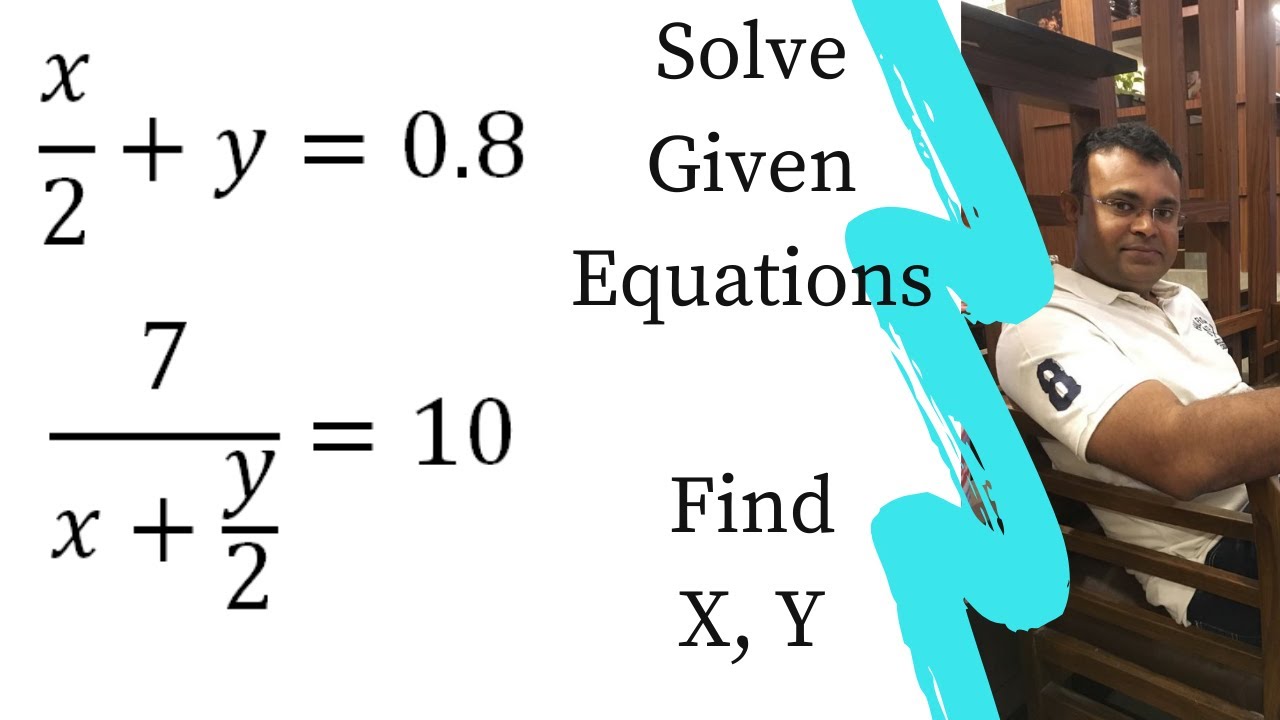



Solve X 2 Y 0 8 7 X Y 2 10 Youtube
Question 2 Solve by Substitution Method 2x 3y = 8 and 3x y = 1 X =2, y=1 X=11/5, y =28/5 x = 1, y = 2 X = 9/5, y = 22/5 Question 3 Solve the inequality 15(x 4) 10(x 4) and write your solution in interval notation O(4, 0 (,4) 4) ( 0,4) A Moving toIs done on EduRev Study Group by Class 10Use the Substitution method to solve the system of equations 3x y = 5 4x 7y = 10 multiply first equation by 4 multiply second equation by 3 thus both equations have same x or y value in this case it is the x value 12x 4y = 12x 21y =



If X Y 6 And 3x Y 4 Then What Is X Y Equal To Quora




10 X Y 5 X Y 5 6 X Y 9 X Y 6 Find Value Of X Y X Y Brainly In
Step 1 Enter the system of equations you want to solve for by substitution The solve by substitution calculator allows to find the solution to a system of two or three equations in both a point form and an equation form of the answer Step 2 Click the blue arrow to submit4x − 2y = 2) Explain how to solve a system of equations with substitution method for both y and x Created by Rose sciencemathematicsen mathematicsenStep 1 Solve one of the equations for either x = or y = We will solve second equation for y Step 2 Substitute the solution from step 1 into the second equation Step 3 Solve this new equation Step 4 Solve for the second variable The solution is (x, y) = (10, 5) Note It does not matter which equation we choose first and which second



Solve The Following Simultaneous Equations Graphically I 3x Y 2 0 2x Y 8 Ii 3x Y 10 X Y 2 Sarthaks Econnect Largest Online Education Community




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo
We use the substitution method when we substitute numbers for variables in an algebraic expression or formula Substitution Method – Example Study the example below that shows how to use the substitution method in systems of equations Example Solve for x and y if 3x 2y = 4 and x 4y = 3 Answer x = 1Start studying Substitution Method Learn vocabulary, terms, and more with flashcards, games, and other study tools Home Browse Create Search Log in Sign up Upgrade to remove ads y = x 2 y = 3x 2 ( 4 , 10 ) 2y = 8 3x y = 6 x ( 23 , 16 ) 3y 4x = 14 y = 2x 3 ( , 40 ) x y = 60 5x 3y = 2 ( 4 , 3 ) 2x 3y = 1 y = xBy substitution method, 3x4y =10 & 2x−2y = 2⇒ 2(x−y) = 2⇒ x−y = 1 ___ (2) ∴ x= y 1 → (1) Substituting in equation (2) ∴ 3x4y = 10 ⇒ 3(y1)4y = 10 ⇒ 3y34y = 10 ⇒7y = 7 ⇒y = 1 ∴ x= 11= 2 ∴ x= 2,y = 1



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15
Solve the following equations by the substitution method x = 3y 19, y = 3x 23 > 10th > Maths > Pair of Linear Equations in Two Variables > Algebraic Methods of Solving a Pair of Linear Equations > Solve the following equatio x = 2, y = 1 Stepbystep explanation 3x 4y = 10 y = x 1 The value of y is given, so plug in (x 1) for y in the first equation 3x 4(x 1) = 10 Expand 3x 4x 4 = 10 Simplify 7x 4 = 10 Add 4 to both sides 7x = 14 Divide both sides by 7 x = 2 Plug in 2 for x in the second equation y = 2 1 y = 1 This will give us a quadratic expression where we can solve for x x2 (x 7)2 = x2 (x2 14x 49) = 109 Simplifying this we get x2 7x − 30 = 0 This can be factorized to (x − 3)(x 10) = 0 giving us the solutions x = 3 and x = − 10 We can then solve for y using the equation y = x 7 If x = 3 then y = 10




Systems Of Equations Substitution Method Ppt Video Online Download




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
From (ii), we get y = 2x 3 Substituting y = 2x 3 in (i) we get 3x 7 (2x 3) 10 = 0 => 3x 14x 21 10 = 0 => 11x = 11 `=> x = 11/ (11) = 1` Putting x = 1 in y = 2x 3 we get `=> ySolve by substitution method 3x 4y = 10, 2x 2y = 2 Given 3 x 4 y = 1 0 — (1) 2 x − 2 y = 2 By substitution method, 2 x − 2 y = 2 ⇒ 2 (x − y) = 2 ⇒ x − y = 1 ∴ x = y 1 → (2)Math, 0525, enrica11 Substitution method xy=10 x=4




3 Systems Of Linear Equations




Ex 3 3 1 I Solve By Substitution X Y 14 X Y 4 Video
Solving system of equation by substitution method, involves solving any one of the given equation for either 'x' or 'y' and plugging that in the other equation and solve that equation for another variable Example 1 2xy=1 3x5y=2 Solution In the given two equations, the first equation has only 'y' term So let us solve for y in the first Here, we have a quadratic and a linear equation which can be solved by the substitution method From the second equation, know y = 3x8 put this in place of y in the first equation We get, 3x 8 = x^22 Rearrange x^2 3x 10 = 0 It can be factorized x^2 5x 2x 10 =0 x(x5) 2(x5) = 0 (x5)(x2) = 0 Therefore, x =5 and x = 2 are the roots of equationBy elimination method 3xy7/112=10 2yx11/7=10 Ask questions, doubts, problems and we will help you




Solve The Equation Graphically X Y 6 3x Y 10 Brainly In




3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall
Finally, substitute the solution for y into the expression for x x = 30 8(4) = 2 x = 2 So the solution to the pair of simultaenous linear equations is (2,2);Solve for x and y using elimination method 10 x 3y = 75, 6x 5y = 11 solve for x,y,zxy2xy1=0;yz3y2z4=0;zx3xz1=0 Solve the following equations by substitution method y= (74x)/ (3) And 2x3y=1 Solve for x and y using substitution method ( 3x )/ ( 2) ( 5y )/ ( 3) = 2, ( x(3x y = 10;




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




X Y X Y 10 Solve The Following Brainly In
Solution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0Substitution Method in Algebra!HELP PLZ! Substitution method class 10 worksheet pdf Printable worksheets and tests Linear equations in two variables 5 4x 7y 19 6 y 6x 11 y x 9 2y 4x 14 7 2x 8y 6 8 x 2y 1 y 7 x 3x 2y 3 Systems of equations substitution method sheet 1 1 5 2 16 8 26 2 6 7 2 2




Solve X And Y X 6 Y 4 1 And 3x 4 X Y 2 7 4 Related Substitution Method Pair Of Linear Equations In Two Variables Edurev Class 10 Question




Pair Of Linear Equations In Two Variables Class 10 Solutions Exercise 3 3
x y = 10 3x y = 64x = 16 x = 4 so, plug 4 back into the xy equation and you get y=6 You are using elimination by adding the y and the yThe elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




Solved Review Exercises Use The Substitution Method To Solve Chegg Com




Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube




Solved Each De In Problems 1 14 Is Homogeneous In Problems Chegg Com



Solve The Following Simultaneous Equations Graphically I 3x Y 2 0 2x Y 8 Ii 3x Y 10 X Y 2 Sarthaks Econnect Largest Online Education Community




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall
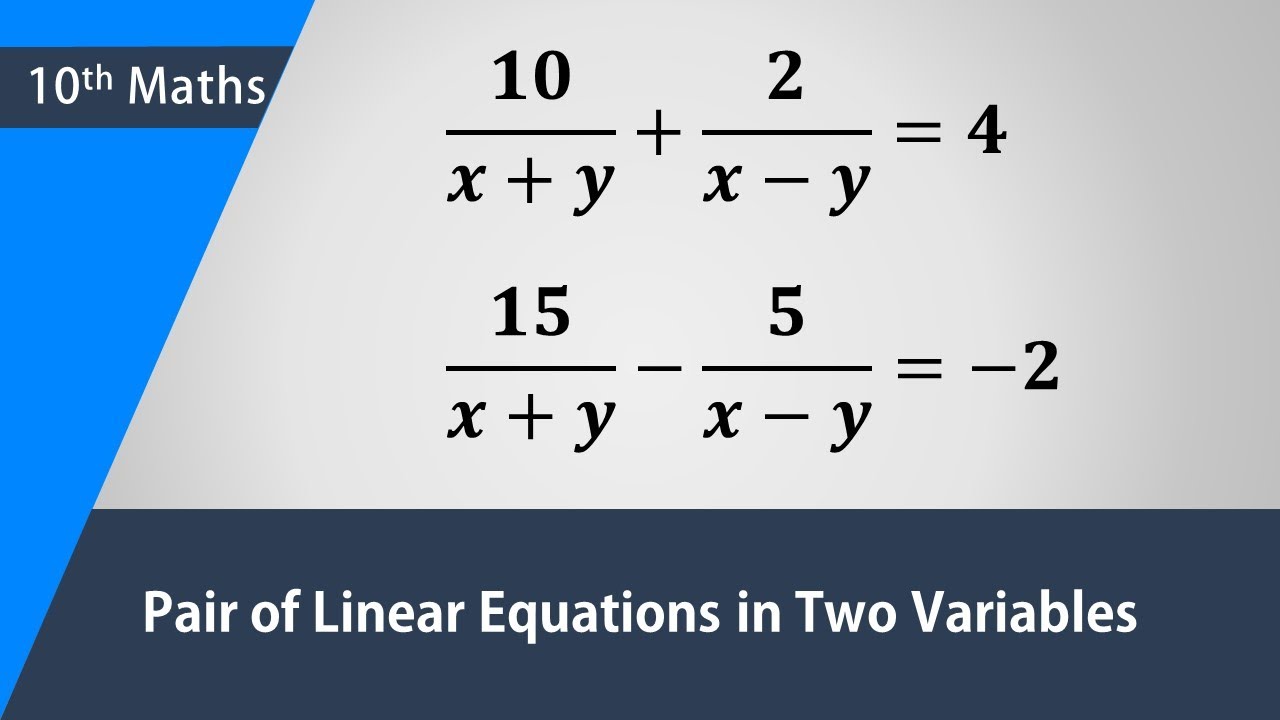



10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve For X And Y Youtube




Solve By Reducing To Pair Of Equations 1 3x Y 1 3x Y 3 4 1 2 3x Y 1 2 3x Y 1 8 Youtube




Ex 3 3 1 I Solve By Substitution X Y 14 X Y 4 Video




Solve The System Of Equations Frac X 2 Y 0 8 And Frac 7 X Y 2 10 And Also Find The Value Of Frac X Y Snapsolve




3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall




3x Y 10 And X Y 2 Problem Set 1 Q3 5 Of Linear Equations In Two Variables Youtube




Ncert Class 10 Mathematics Chapter Wise Questions And Answers And Solutions
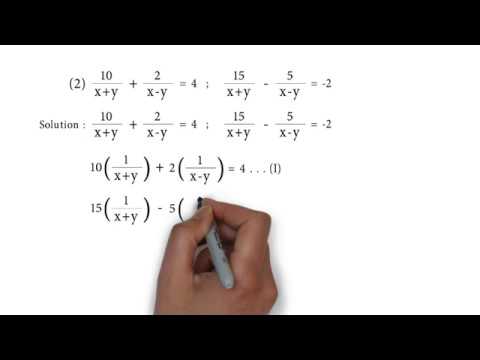



10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube




Ex 12 1 5 Maximise Z 3x 2y Subject To X 2y 10



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora



3x Y 2 0 2x Y 8




1 Solve The Following Pair Of Linear Equations By The Substitution Method 1 X Y
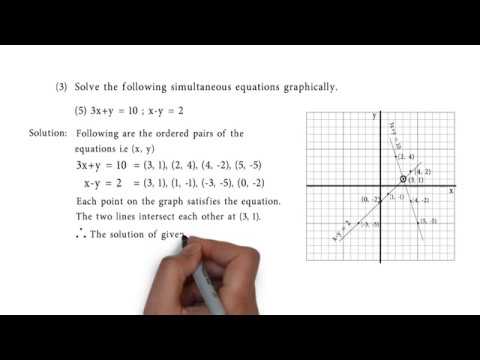



3x Y 10 And X Y 2 Problem Set 1 Q3 5 Of Linear Equations In Two Variables Youtube




3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall



3x Y 2 2x Y 3 Solve Graphically



The Elimination Method




Solve By Substitution 4x 2y 10 And X Y 13 Youtube




X Y 2 Solve Duparah
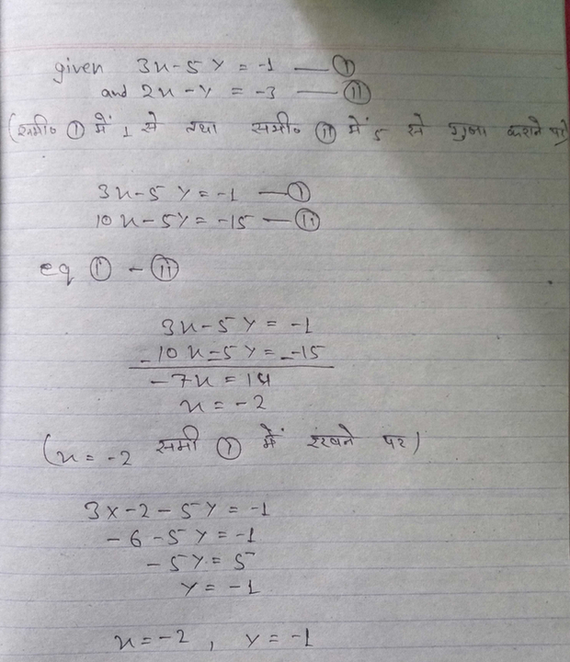



Solve By Substitution Method 3x 5y 1 And 2x Y 3 Scholr



Solve The Following Pairs Of Linear Equations By The Elimination Method And The Substitution Method Ii X 2 2y 3 1 And X Y 3 3 Sarthaks Econnect Largest Online Education Community




10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve The Pair Of Linear Equations Youtube



If 3x 2y 16 Y Z 13 And 5x Z 2 Then What Is The Value Of X Y Z Quora




J19




Chapter 1 1st Order Linear Differential Equations




Ex 3 6 1 Vii And Viii Class 10 Ncert Solutions Maths




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solved Use Elimination To Solve Each System Of Equations 1 Chegg Com




Solving Systems Of Equations Using Elimination Ppt Download




Solve The Following Pair Of Linear Equation By Substitution Method I X Y 2 3x 2y 16 Brainly In
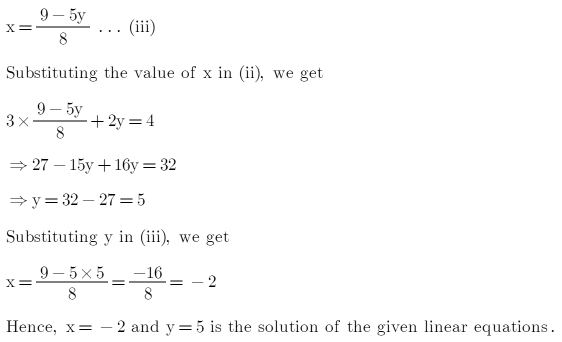



By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll




3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solved 1 Find The General Solution Of Differential Equation Chegg Com




Solve 3x 4y 10 2x 2y 2 By The Method Of Elimination



X Y 25 And X Y 5 What Is The Value Of X And Y Quora



3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall



If X Y 5 And Xy 10 What Are The Value Of X And Y Quora



2x Y 10 Graph



Solve The Following Systems Of Equations X Y 5xy 3x 2y 13xy Sarthaks Econnect Largest Online Education Community




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt




Q3e 3x Y 10 X Y 2 Solve The Following Simultaneous Equation Graphically




X Y 3 And 3x 2y 10 Solve Using Substitution Method Brainly In




Solve 3x 4y 10 And X Y 1 Brainly In
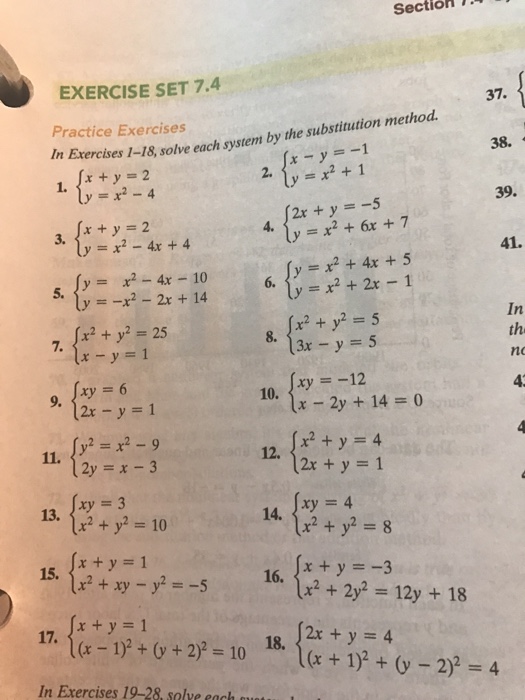



Solved Solve Each System By The Substitution Methos X Y Chegg Com
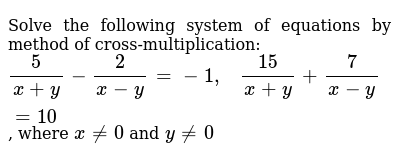



Solve The Following System Of Equations By Method Of Cross Multiplication 5 X Y 2 X Y 1 15 X Y 7 X Y 10 Where X 0 And Y 0




30 Days Free Access Get Access Homework Help What S Your Question Pricing Log Insign Up Ask A Question All Subjects Accounting Algebra Anthropology Architecture Astronomy Biology Business Calculus Chemistry Communications Computer Science



What Is The Equation To The Circle Circumscribing The Triangle Formed By The Lines X Y 2 0 2x 3y 4 0 3x Y 6 0 Quora




3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall



3x 4y 10 And 2x 2y 2




X Y 10 X Y 2 Cross Multiplication Elimination Substitution Brainly In




Ex 3 3 Qno 1 1 Solve The Pair Of Linear Equations X Y 14 X Y 4 By Substitution Method Class 10 Youtube




3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall




Best Answer 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve Using Equation Reducible To A Pair Of Linear Brainly In




1 Systemsofequationsandinequal Ities X 5 Y 25 25 5 Figure1 Consistent X Acirc Circ Rsquo 3y Acirc




Solve By Substitution Method X Y 2 3x 2y 16 Brainly In



If X Y 2 Then What Is The Value Of X Y 6xy Quora




X Y 2 Solve Duparah




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




Solved Problems In Differential Equations 2500 Solved Problems In Differential Docsity




Name Fased Al Hamvn Own Ee1 Quiz4 Solve The Equations p 23 Solutions Xy 2 4x 3y 11 2x Y Homeworklib
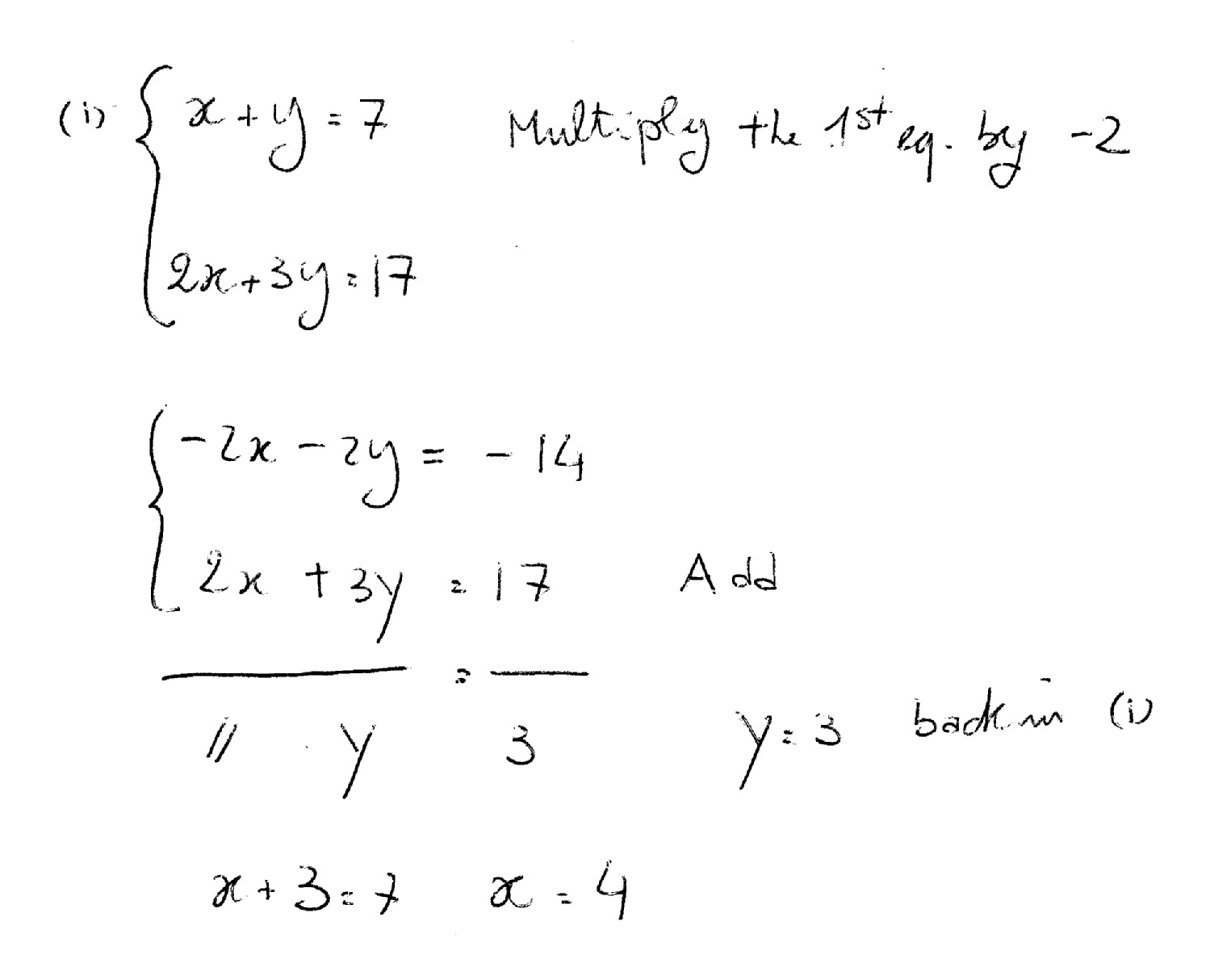



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic




3x Y 10 X Y 2 7857 Solve 3x Y 10 X Y 2 Patmongjpwall
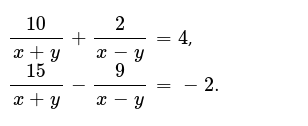



10 X Y 2 X Y 4 15 X Y 9 X Y 2




X 2 2y 3 1 And X Y 3 3 Solve By Elimination Method Brainly In
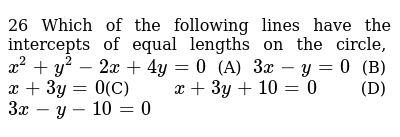



3x Y 10 X Y 2 Simultaneously
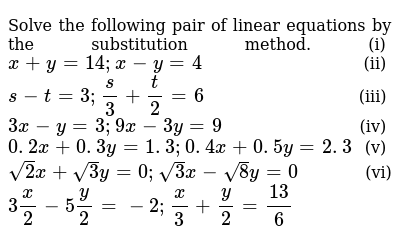



Solve The Following Pair Of Linear Equations By The Substitution Method I X Y 14 X Y 4 Ii S T 3 S 3 T 2 6 Iii 3x Y 3 9x 3y 9 Iv 0 2 X 0 3 Y 1 3 0 4 X 0 5 Y 2 3 V Sqrt 2 X Sqrt 3 Y 0 Sqrt 3 X Sqrt 8 Y 0 Vi 3x 2 5y 2 2 X 3 Y 2 13 6



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3


