年の最高 球体 表面積 公式 球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和 球体表面积公式 怎样计算球体14/1/ 円の半径=球の周の長さの 1 4 = 1 2πr 半径 1 2πr の円と見立てて面積を求めると, 面積= 1 2πr × 1 2πr × π = π2 4 πr26/3/21 よって,球帯の表面積は S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ S=2\pi r^2\int_{\theta_1}^{\theta_2}\cos\theta d\theta S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ (ただし, θ 1 \theta_1 θ 1 は球帯の底面の緯度, θ 2 \theta_2 θ 2 は球帯の天面の緯度)
椭圆球表面积公式球体表面积公式
球体 表面積 公式 中学
球体 表面積 公式 中学-球の体積と表面積 東京大学大学院数理科学研究科・教授 古田幹雄 1 円の面積と円周の長さ 半径rの円の面積はˇr2 です。 グラフv = ˇu2 のu = rにおける接線の傾きを求めてみま す。すると、答えは2ˇrとなります。これは半径rの円周の長さです。つまり、円の面積球の表面積 \(\pi D^2\) 球の体積 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3\) 球の質量 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3 \rho\) 球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積)



官方双语 为什么球的表面积是同样半径圆的面积的四倍 哔哩哔哩 つロ干杯 Bilibili
12/5/15 球の体積の公式を忘れちゃったときに参考にしてみて。 球の体積の公式を1発で覚える方法 「球の体積の公式」を暗記する方法を伝授しよう。 3分の4 × 円周率 × 半径の三乗 という公式はつぎの語呂を使えばおぼえられちゃうよ。11/2/21 回転体の体積 関数 をx軸周りに回転させてできる回転体の体積V 求め方②球の表面積を用いる 考え方 図のように薄い球殻を集めると球体になる. 球の表面積は なので, 球殻1つの体積は(表面積)×(厚さ)= 計算 最後に 全記事をまとめてあります.物理というよりかは数学ですね。 イ19/2/21 球体 表面積 公式 8524球体 表面積 体積 公式
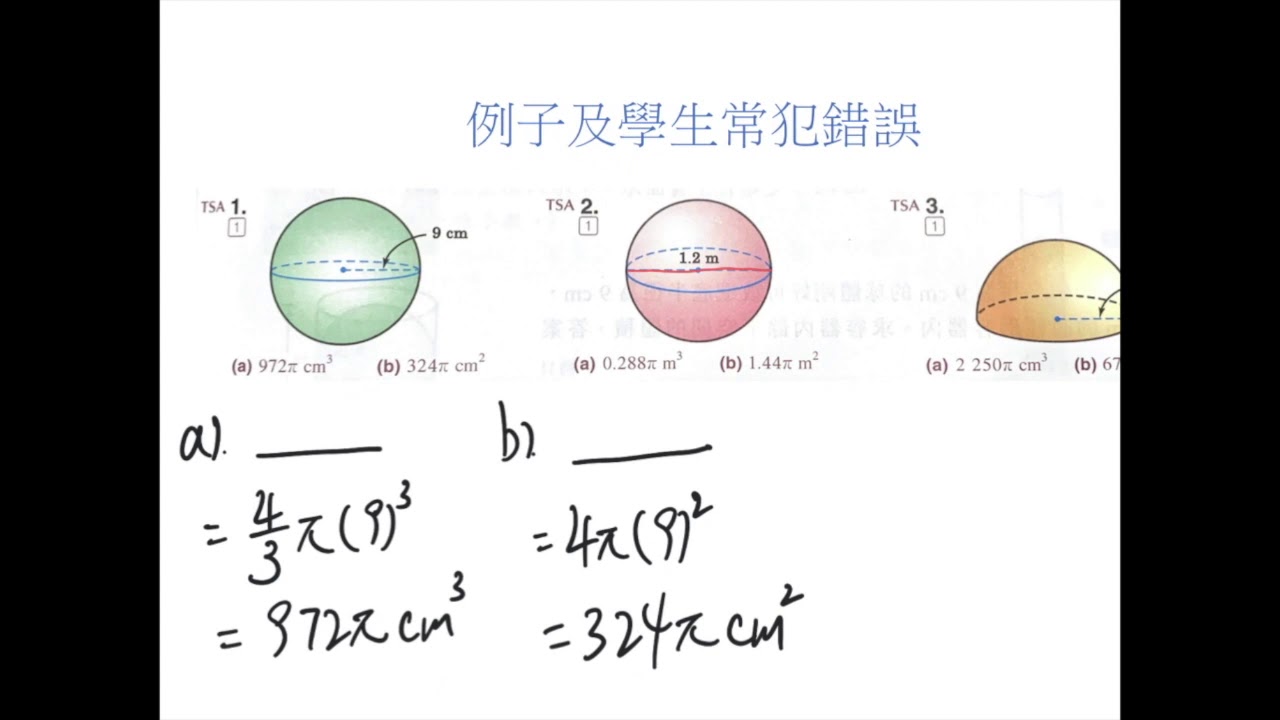
回転体の表面積も求めよう! では次,曲線をx 軸やy 軸のまわりに回転してできる回転体の曲面の表 面積を求める公式についても解説しておこう。 (Ⅰ) について,微小区間x, +Δ における 微小な曲面の表面積 ΔS は,図12 より6/9/16 まずは、球の表面積の公式を使います。球の表面積の公式は4πr 2 でしたね。 よって、 4π×3 2 =36π です。しかし、今回は半球なので、36πの半分となり、 18π・・・① となります。 まだこれで終わりではありません! 半球の底の部分を足していませんね!12/2/21 球体表面積公式 球体表面積公式(球の表面積) = 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。 球の体積 は、 身の上に心配あるので、参上。 球の表面積は、心配ある事情。
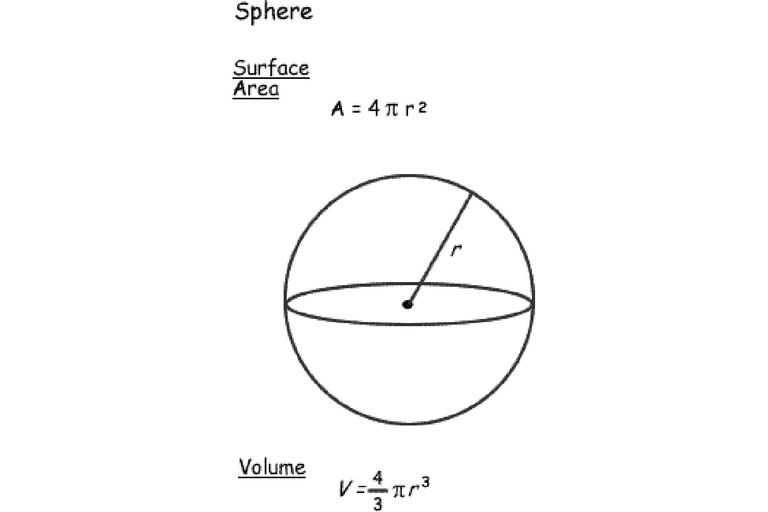
6/3/21 球の体積と表面積の公式 半径 r r r の球の表面積は S = 4 π r 2 , S=4\pi r^2,\ S = 4 π r 2 , 球の体積は V = 4 3 π r 3 V=\dfrac{4}{3}\pi r^3 V = 3 4 π r 3 である。よって球の表面積は外接円柱側面の面積に等しい、 とう趣旨を主張している。 12 節回転体の体積 任意の面を軸の回わりに回転させた回転体の体積公式は、 西洋流ではバッポス = ギュルダンの公式と呼ばれる。関も、 と (3 において、公式を4) 「体積=面積公式計算 平面図形の面積(a),周長(l)および重心位置(g) p11 平面図形の性質 p12 立体の体積(v),表面積(s)または側面積(f)および重心位置(g) p12




證明球體體積公式 Youtube




球的表面积和体积公式是什么
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。球の表面積が円の面積の4倍であることの証明 About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features立方体の表面積 V = 6a2 V = 6 a 2 表面積 = 一辺 × 一辺 × 6



球体的表面积公式及性质 中国教育网




外接球体积的常见套路 几何 知乎
15/5/15 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するための語呂は、よって、球の体積Vは、円の面積をx 方向に積分すると、V=2∫0rπ(r2-x2) dxより、 V=2πr2x-(x3/3)0r=(4/3)πr3を導くことができる。 ②球の表面積の公式の求め方(1)表面積 (上辺・底辺含まず) S = π (2 r h 2 r 2 − h 2)
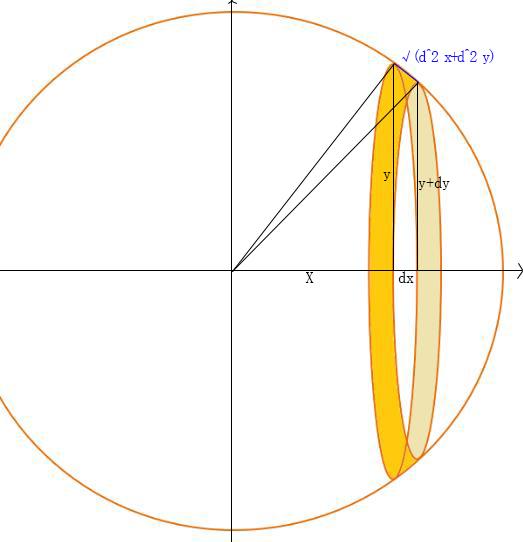



用积分推导球的表面积有哪些方法 球的表面积公式怎么来的 德涵网



1
(球の表面積) = 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。 球の体積 は、 身の上に心配あるので、参上。 球の表面積は、心配『球と円柱について』(ギリシア語 Περὶ σφαίρας καὶ κυλίνδρου )は、紀元前225年ごろアルキメデスにより発表された2巻からなる著作 。 最も注目すべきは、球面の表面積や球体の体積、円柱のそれにあたる値を見つけ出す方法が詳しく書かれていることであり、アルキメデスはこれ楕円体の体積 体積 V = 4π a b c /3 楕円体の表面積 (楕円面の表面積) a ≧ b ≧ c ならば、表面積は楕円積分を用いて次式で与えられる。




球的表面积公式是什么 球体积 表面积公式是




胶囊罐体 球冠高等于柱体半径 体积 表面积计算公式 三贝计算网 23bei Com
6/4/21 こんにちは!この記事をかいているKenだよ。豚肉を今日もいためたね。 球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。 つまり、 4 × 円周率 × 半径 × 半径 球体 表面積 求め 方" />球の表面積の求め方公式 半径 のV = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin球の半径から体積と表面積を計算します。 一部が欠けた球の体積 一部が欠けた球の体積 一部が欠けた球の体積と表面積を計算します。 弓形の回転体の体積 弓形の回転体の体積 弓形の回転体の体積と底面積と表面積を計算します。



Nlopv5ztd519 M




球冠表面積公式 若球半徑是r 球冠的高是h 球冠面積是s 則s 華人百科
た円の面積や球の体積・表面積を求めるための公式と して生徒は受け止め,これらの式を暗記すればよいと みる傾向が強い。 円の面積,球の体積や表面積の公式を導く過程には, 様々な数学的なアイデ28/2/18 円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事14/1/ 球体の表面積 球体の表面積S = 4πr 2 目標: 積分 を用いて上式を導出する 方法を2つ考えました. 求め方1:微笑の範囲を考える方法 求め方2:球体の体積を用いる方法




球體表面積球體 表面積 體積 Vhjk



如何不用微積分算個球 中科院物理所 微文庫
球の表面積を求める公式は、S = 4πr^2 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。11/1/21 球体を描いて保存する Powerpoint16 初心者のためのoffice 球の体積 表面積 公式の覚え方は語呂合わせでS:球の表面積ってどうやって求めるのだろう。 s:円の場合は細かな三角形に分割して面積を求めたよ。 円錐の側面積も三角形に分けると簡単に求めることがでる。球でも、同じじゃないかな。 s:そういえば、地球儀を作る時に細かな三角形を張り合わせるでしょう。
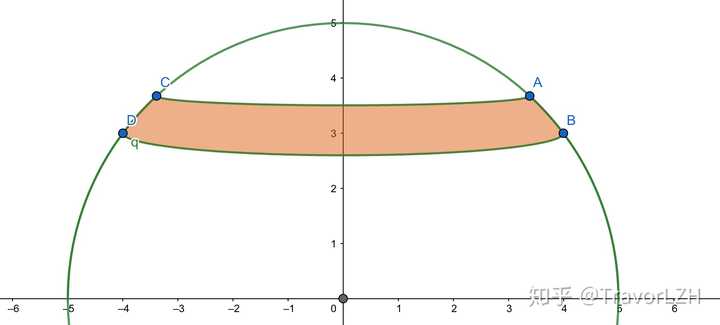



如何使用高中知识推导球体表面积 知乎




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org
元々球体の表面にある部分のk1とk2での表面積をs(k1)、s((k2)で表したとき、 s(k1) : s(k2) はどの様になるか? 完璧に球体であるリンゴを半分の半分としたリンゴのそれぞれの皮をむいたら、さてどちら の皮の面積がどれだけ大きくなるか想像してみよう。球体 体積 求め 方もくじ 1 球の体積を出す公式での求め方 11 円柱と球の体積の関係;円すい(円錐)の体積の求め方と問題 図形の面積(体積)や周りの長さを文字式にする問題まとめ 補足 上の練習問題で、半径が2cmの球は半径が1cmの球に比べて、体積は8倍、表面積は4倍になっています。球の表面積は 4×円周率×半径×半径=表面積 で求めることができます。 円周率をπ、半径をr、表面積をSとすると、 S=4πr 2 となります。




椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



圆球表面积 球体表面积的公式证明 篆体字转换器
球の表面積の場合は、 球面の全てを覆うように積分範囲を指定する必要があったが、 弓形領域の半分の領域 弓形領域の半分の領域 (黄色) の面積を求める場合は $\phi$ に関する積分範囲を $\alpha$ にすると、その領域が覆われる。




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org




球體表面積公式sphere Java Mvc Liudong




圆锥与球与圆柱



球的体积公式 万图壁纸网




求球体积公式 圆球的体积公式 求球体积积分公式



椭圆球表面积公式球体表面积公式



球的表面积计算公式例子 求球表面积公式 公式学习
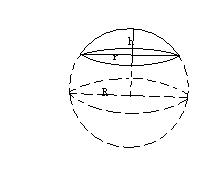



球缺 维基百科 自由的百科全书



球体体积与表面积公式有何巧妙的内在联系 哔哩哔哩 Bilibili



體積公式 台灣word
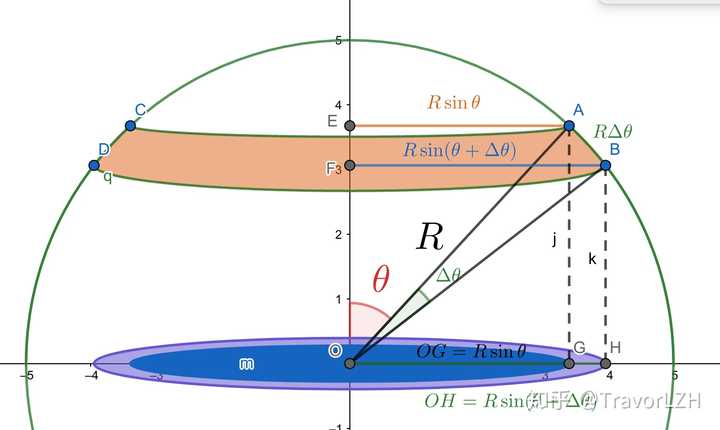



如何使用高中知识推导球体表面积 知乎



球体的表面积体积计算公式是什么 尚书坊



高中数学第一章空间几何体1 3空间几何体的表面积与体积2球的体积和表面积 教案 新人教a版必修2 Doc 课件巴巴kejian Com 课件巴巴kejian Com




各類幾何體的體積與表面積的計算問題 每日頭條



球的体积公式和表面积公式 中国练字网




球表面積公式球體表面積 百度百科 Kmbymh



阿基米德是如何发现球体体积和表面积公式的 哔哩哔哩 つロ干杯 Bilibili



球体表面积公式球体表面积球体表面积 公式证明 爱华网




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com



球体面积公式推导图解 搜狗图片搜索
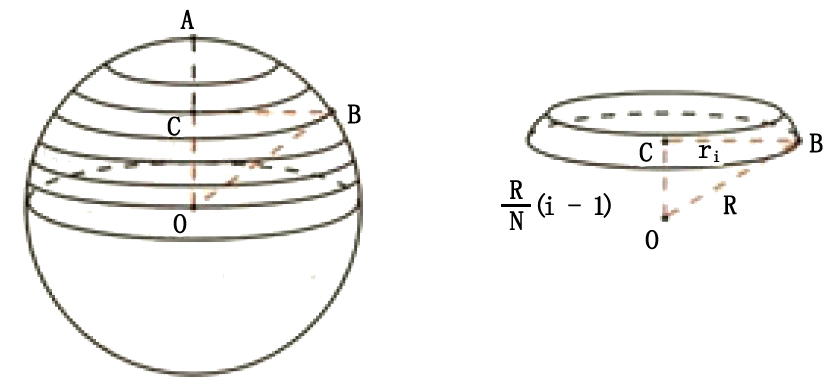



球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客




球の体積と表面積 公式と計算問題と証明 Irohabook




球の表面積の求め方 公式と計算例




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球体计算公式大全 西瓜视频搜索



官方双语 为什么球的表面积是同样半径圆的面积的四倍 哔哩哔哩 つロ干杯 Bilibili



圆球表面积公式的推导圆球体积公式的推导过程




Avk8t66yhnqn8m
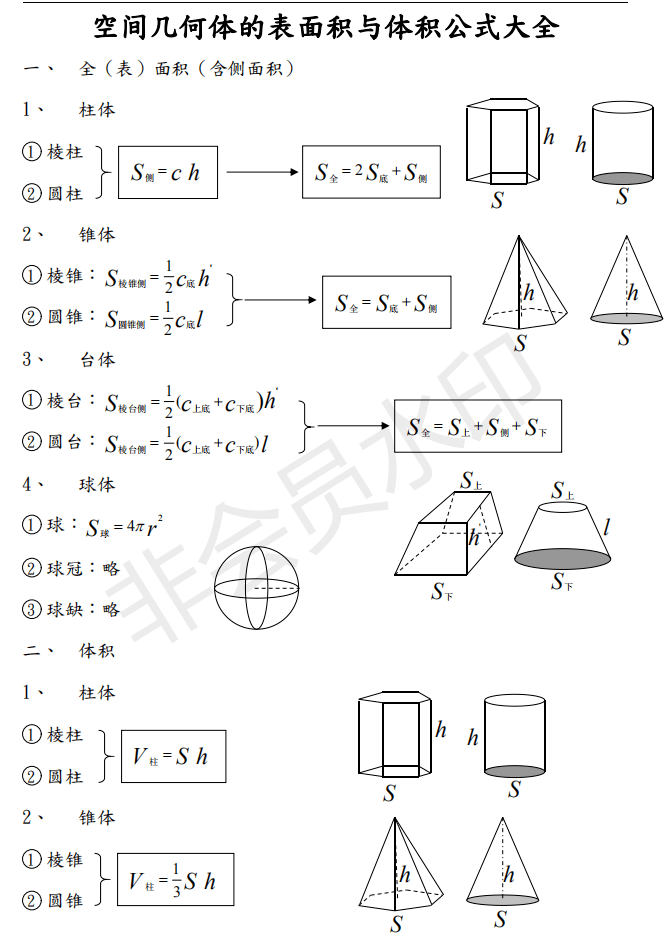



22高三数学第一轮复习 空间几何体的表面积与体积公式大全 整理




球体的表面积和体积的计算公式 星火网校



表面积计算公式比表面积定义公式 所有表面积公式



Q Tbn And9gctku R5xzpdmwkdjs1wzabajezbi10itywbdbzcvyi Usqp Cau



圆台体积公式 万图壁纸网




球体积表面积公式
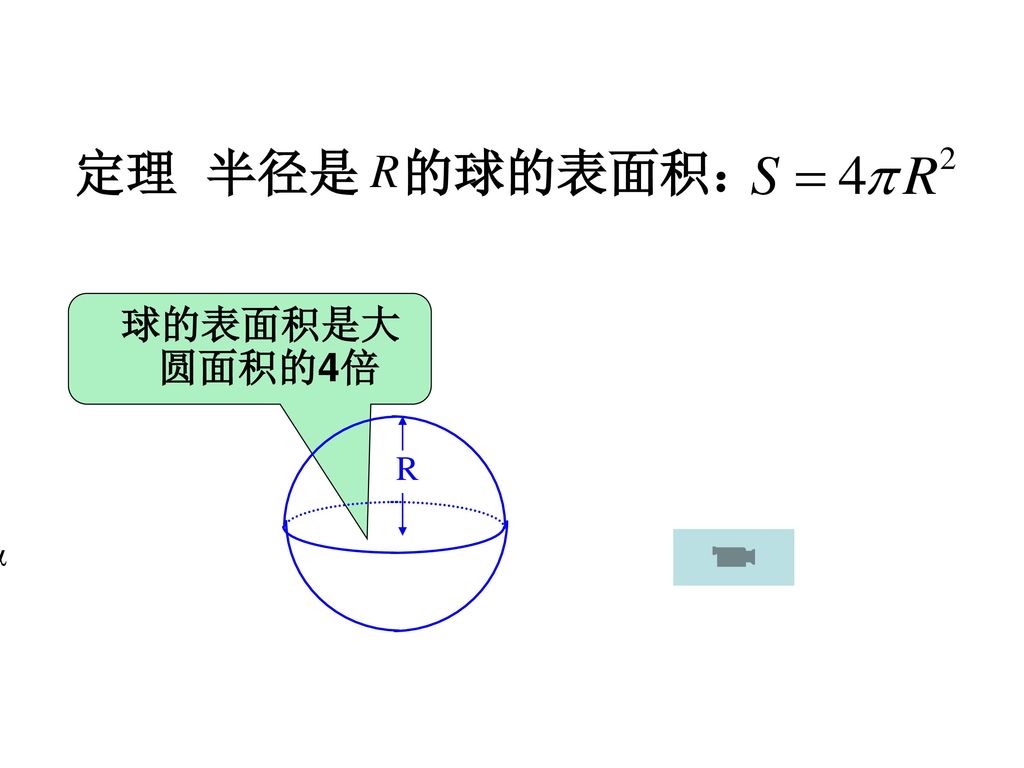



球的体积和表面积 西伯利亚 Ppt Download



球的表面积 球的表面积画法



球体面积公式图解 圆球的表面积公式 公式学习




球体表面积推导定积分 怎么用定积分证明球体表面积公式 三人行教育网 Www 3rxing Org



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社




Word中如何插入球体表面积公式 百度经验




椭球体表面积公式 椭球表面积怎么算 三人行教育网 Www 3rxing Org




球缺体积和球冠表面积的计算公式及应用 晨起尘又落 Csdn博客




球体表面积公式 球体体积公式 环球信息网




Word中如何插入球体表面积公式 百度经验




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫



球的表面積的求法 中學數學課 隨意窩xuite日誌




半球体积 表面积 截面积 球面积在线计算器 三贝计算网 23bei Com




3种方法来计算球体的半径



不完整球体表面积求不规则半球体的表面积




圆球表面积计算器软件 圆球表面积计算器下载 V1 0 计算器下载站



3




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网



圆球表面积公式推导球体的体积公式 表面积公式的推导




球の表面積と体積の公式 数学fun
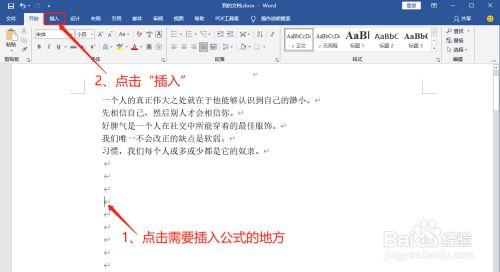



Word中如何插入球体表面积公式 百度经验



球的表面积公式 球的表面积公式画法




旋轉體的側表面積040 正修科技大學微積分課程6 5 Youtube



在球的体积公式中 为什么会出现三分之四这个奇怪的系数 体积 公式 系数 新浪新闻



球体表面积公式 100查分网




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




用感覺理解球體表面積公式 Youtube




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科




無料ダウンロード球表面積公式 ページを着色するだけ




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com



用微积分解答半径为a的球的表面积 作业 慧海网



球體體積 總表面面積 Youtube



球的表面积公式 球的表面积公式画法



数学一分钟球的体积公式推导证明 哔哩哔哩 つロ干杯 Bilibili



球體的體積及表面面積 哔哩哔哩 Bilibili




球體的體積球體 360百科翻譯此網頁 Gahzw




球の体積と表面積 Youtube




球面積積分球的體積 Itha




球體表面積及體積的推導 每日頭條



球的表面积公式推导 万图壁纸网



基本形狀和3d圖形的數學公式




Ve6kx8wvmlsorm




3种方法来计算球体的半径



1




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球體積的前世今生 每日頭條



球体体积公式推导图解 万图壁纸网




用感覺理解球體表面積公式 Youtube




7 3b球體的表面面積 Youtube



球体表面积公式 怎样计算球体的表面积



球表面积公式推导图解 第1页 要无忧健康图库



半球表面积和体积公式 求半圆的体积公式和表面积公式 三人行教育网 Www 3rxing Org




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題


