An ellipse is one of the shapes called conic sections, which is formed by the intersection of a plane with a right circular cone The general equation of an ellipse centered at (h, k) ( h, k) is (x − h)2 a2 (y − k)2 b2 = 1 ( x − h) 2 a 2 ( y − k) 2 b 2 = 1 when the major axis of the ellipse is horizontalThe given equation is x2 25 y2 9 = 1 x 2 25 y 2 9 = 1 Compare this to the standard form of the equation of a horizontal ellipse centered at the origin given by x2 a2 y2 b2 =1 x 2 a 2 y #3 A solid has a base in the form of the ellipse x^2/25 y^2/16 = 1 Find the volume if every cross section perpendicular to the xaxis is an isosceles triangle whose altitude is 6 inches #4 Use the same base and cross sections as #3, but change the axis to the yaxis
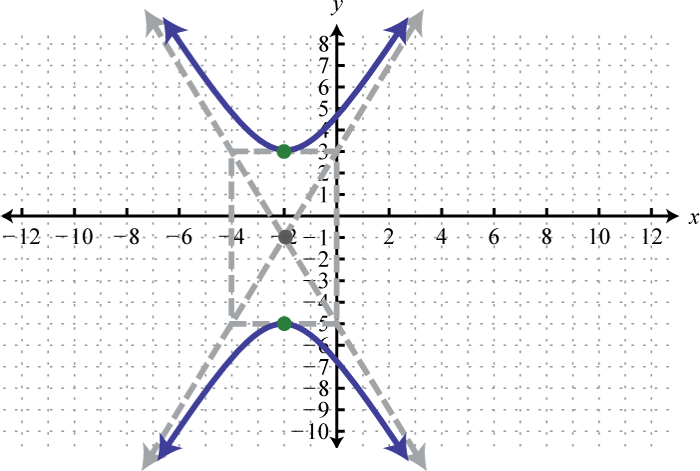
Hyperbolas
((25)/(4)x^(2)-(1)/(9)y^(2))
((25)/(4)x^(2)-(1)/(9)y^(2))-Compare and contrast the graphs of the equations x 2 4 − y 2 9 = 1 x 2 4 − y 2 9 = 1 and y 2 9 − x 2 4 = 1 y 2 9 − x 2 4 = 1 187 Explain in your own words, how to distinguish the equation of an ellipse with the equation of a hyperbola The standard form of the equation for an ellipse is given by (x −xc)2 a2 (y − yc)2 b2 = 1 with the point (xc,yc) representing the center, the value a representing the horizontal semiaxis length, and the value b representing the vertical semiaxis length From inspection of the original equation, we can see that xc = 0 and yc = 0



1
If a point P (x, y) moves along the ellipse (x^2 / 16) (y^2 / 25) = 1 and C is the centre of the ellipse, then the sum of maximum and minimum values of CP isA) (5cos Ѳ , 3sin Ѳ) (5 sin Ѳ,3 cos Ѳ) b) (5cosѲ,3sinѲ) , (5sinѲThe graph is an ellipse with center ( 0, 0 ) Rewriting the equation, we have x 2
Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepExample of the graph and equation of an ellipse on the The major axis of this ellipse is vertical and is the red segment from (2, 0) to (2, 0) The center of this ellipse is the origin since (0, 0) is the midpoint of the major axis The value of a = 2 and b = 1 The major axis is the segment that contains both foci and has its endpoints on91k views asked in Class XII Maths by vijay Premium (539 points) The area of the region bounded by the ellipse x 2 /25y 2 /16 = 1 is (a) π squnits (b) π 2 squnits (c) 16π 2 sq units (d) 25π sq units applications of integrals
Graph (x^2)/25 (y^2)/9=1 x2 25 y2 9 = 1 x 2 25 y 2 9 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an ellipse or hyperbola requires the right side of the equation be 1 1 x2 25 y2 9 = 1 x 2 25 y 2 9 = 1 This is the form of an ellipse Use this form to determine the valuesCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyYintercepts (0, 4) and (0, 4)




Ex 8 1 4 Find Area Bounded By Ellipse X2 16 Y2 9 1



Q Tbn And9gcqgl Gfupobx9xdqlsisy B Ngrrktivrdpczi6s62fn3ggjaud Usqp Cau
Example 9 Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the latus rectum of the ellipse x225 y29 = 1 Given 𝑥225 𝑦29 = 1 Since 25 > 9 Hence the above equation is of the form 𝑥2𝑎2 X^2/25 y^2/9 = 1 Find the equation of the ellipse with the following properties The ellipse with xintercepts (2, 0) and (2, 0); 12 16x2 25y2 = 400 13 9x2 y2 = 18 14 x2 4y2 = 12 In problems 15–16, write an equation for the graph 15 16 In problems 17–, find the standard form of the equation for an ellipse satisfying the given conditions 17 Center (0,0), horizontal major axis
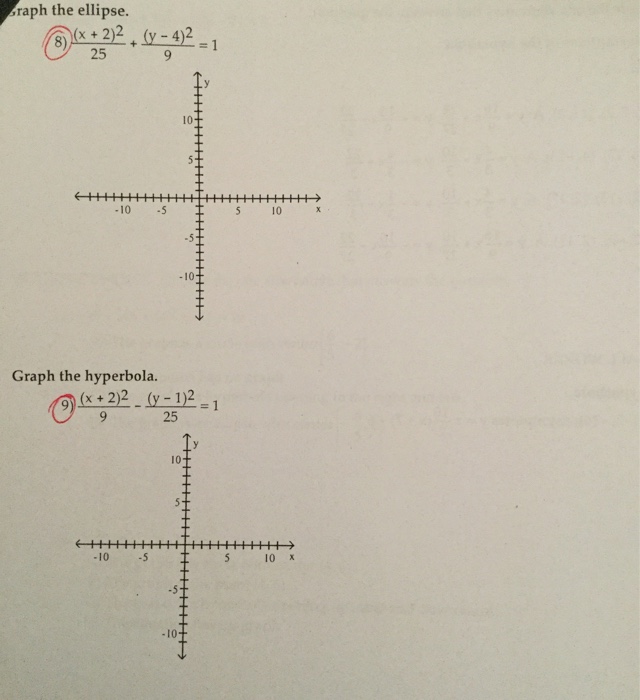



Solved Graph The Ellipse X 2 2 25 Y 4 2 9 1 G Chegg Com
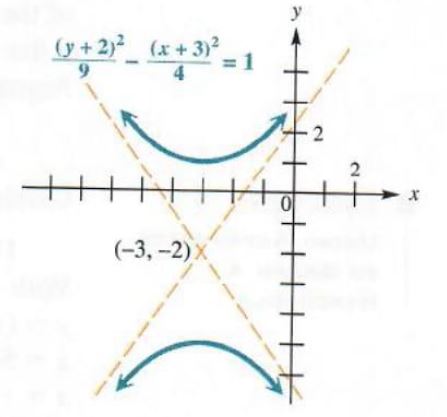



Solve Ellipse And Hyperbola Step By Step Math Problem Solver
73 The conjugate of the hyperbola x 2 a 2 − y 2 b 2 = 1 is x 2 a 2 − y 2 b 2 = − 1 Show that 5 y 2 − x 2 25 = 0 is the conjugate of x 2 − 5 y 2 25 = 0 74 The eccentricity e of a hyperbola is the ratio c a, where c is the distance of a focus from the center and a is the distance of a vertex from the center Find the slope of the tangent line to the ellipse x^2/36 y^2/49 =1 at the point (x,y) slope =_______ Are there any points where the slope is not defined?1 Answer to Find eccentricity of the ellipse x^2/25 y^2/9 =1, Find eccentricity of the ellipse x^2/25 y^2/9 =1



Find The Coordinates Of Foci The Vertices Length Of Major And Minor Axes The Eccentricity And The Latus Rectum Of The Ellipse Sarthaks Econnect Largest Online Education Community




Any Ordinate M P Of The Ellipse X 2 25 Y 2 9 1 Meets The
Click here👆to get an answer to your question ️ A point P on the ellipse x^2/25 y^2/9 = 1 has the eccentric angle pi/8 The sum of the distance of P from the two foci isX 2 ––– 25 y 2 ––– 9 = 1;Answer to Find the center and foci of the ellipse x^2/25 y^2/9 = 1 By signing up, you'll get thousands of stepbystep solutions to your




Ex 11 3 5 X2 49 Y2 36 1 Find Foci Eccentricity Ex 11 3
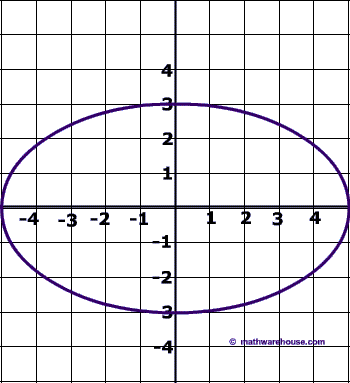



Equation Of An Ellipse In Standard Form And How It Relates To The Graph Of The Ellipse
Solution set for (x,y) is (0,5), (4,3) and (4,3) As 1/2x^2=y5, we have x^2=2*(y5)=2y10 Putting this in x^2y^2=25, we get 2y10y^2=25 or y^22y15=0 ie y^2X^2/25y^2/9=1 Recall from Section 34 that the circle x^2 y^2 = r^2, whose center is at the origin, can be translated away from the origin so that the circle (x h)^2 (y k)^2 = r^2 has its center at (h, k) In a similar manner, an ellipse can be translated so that its center is away from the origin IN SIMPLEST TERMSAn equation of an ellipse is given x^2/25 y^2/9 = 1 (a) Find the vertices, foci, and eccentricity of the ellipse vertex x, y (smaller value), vertex x,y (larger value) focus x,y (smaller) focus x,y (larger) (b) Determine the length of the major axis (c) Determine the length of the minor axis (d) sketch the graph Who are the experts



Www Nrcs Net Downloads T7 2 hw odds and evens3 Pdf




Find An Equation For The Hyperbola Described 6 Chegg Com
Consider the ellipse x^2/25 y^2/9 = 1 with centre C and P is a point on the ellipse with eccentric angle 45° asked in Mathematics by SudhirMandal ( 536k points) ellipseTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Consider an ellipse `x^2/25y^2/9=1` with centre c and a point P on it with ecc2 Answers Andrew Lewis answered you are trying to relate to a 3 dimensional object with a 2 dimensional equation, not impossible but a royal pain in the kazoo I have just spent over an hour on your question and have determined that I dont have




Solved Find The Vertices The Ellipse X 2 25 Y 2 9 1 Chegg Com




Example 9 X2 25 Y2 9 1 Find Foci Vertices Eccentricity
Free Hyperbola Vertices calculator Calculate hyperbola vertices given equation stepbystepGraph (x^2)/9 (y^2)/25=1 x2 9 − y2 25 = 1 x 2 9 y 2 25 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an ellipse or hyperbola requires the right side of the equation be 1 1 x2 9 − y2 25 = 1 x 2 9 y 2 25 = 1 This is the form of a hyperbola Use this form to determine the 1 The equation represents an ellipse only if 2 If any tangent to the ellipse intercepts equal length l on the axes, then l equals to 3 An ellipse has its axes along coordinate axes The distance between its foci is 2h and the focal distance of an end of the minor axis is k The equation of the ellipse is 4




A Tangent To The Ellipse X 2 25 Y 2 16 1 At Any Point P Meets The Line X 0 At A Point Q Let R Be The Image Of Q



If E Is The Eccentricity Of The Ellipse X 2 25 Y 2 9 1 And If E2 Is The Eccentricity Of The Hyperbola 9x 2 16y 2 144 Then E1e2 Is Sarthaks Econnect Largest Online Education Community
Algebra > Quadraticrelationsandconicsections> SOLUTION sketch the graph of each ellipse 1x^2/9y^2/4=1 2x^2/9y^2=1 3x^2y^2/4=1 4y^2/4x^2/25=1 5y^2/9X^2/16=1 6x^2/25y^2=1 7x^2y^2/9=1 8x^2y^2/25=1 9x^2/9y^2=1 Log On (16 河南 #11) A, B A,B A, B 分别为椭圆 C x 2 25 y 2 9 = 1 \displaystyle{C{x^2\over25}{y^2\over 9}=1} C 2 5 x 2 9 y 2 = 1 的左右顶点, ℓ \ell ℓ 交 C C C 于相异的 M, N M,N M, N 两点, 又 k (A M) k (B N) = 1 9 k(AM)k(BN)=19 k (A M) k (B N) = 1 9 (i) 证明 ℓ \ell ℓ 过定点;(ii) 求 (A M N − B M N




Solved For The Ellipse Frac X 2 25 Frac Y




Vertices Direction Of A Hyperbola Example 2 Video Khan Academy
Hyperbola Calculator This calculator will find either the equation of the hyperbola (standard form) from the given parameters or the center, vertices, covertices, foci, asymptotes, focal parameter, eccentricity, linear eccentricity, latus rectum, length of the latus rectum, directrices, (semi)major axis length, (semi)minor axis length, xThe point on the ellipse x^2 /25 y^2 /9 = 1 whose eccentric angles differ by a right angle??2 5 x 2 9 y 2 = 1 Multiply both sides of the equation by 225, the least common multiple of 25,9 Multiply both sides of the equation by 2 2 5, the least common multiple of 2 5, 9 9x^ {2}25y^ {2}=225 9 x 2 2 5 y 2 = 2 2 5 Subtract 25y^ {2} from both
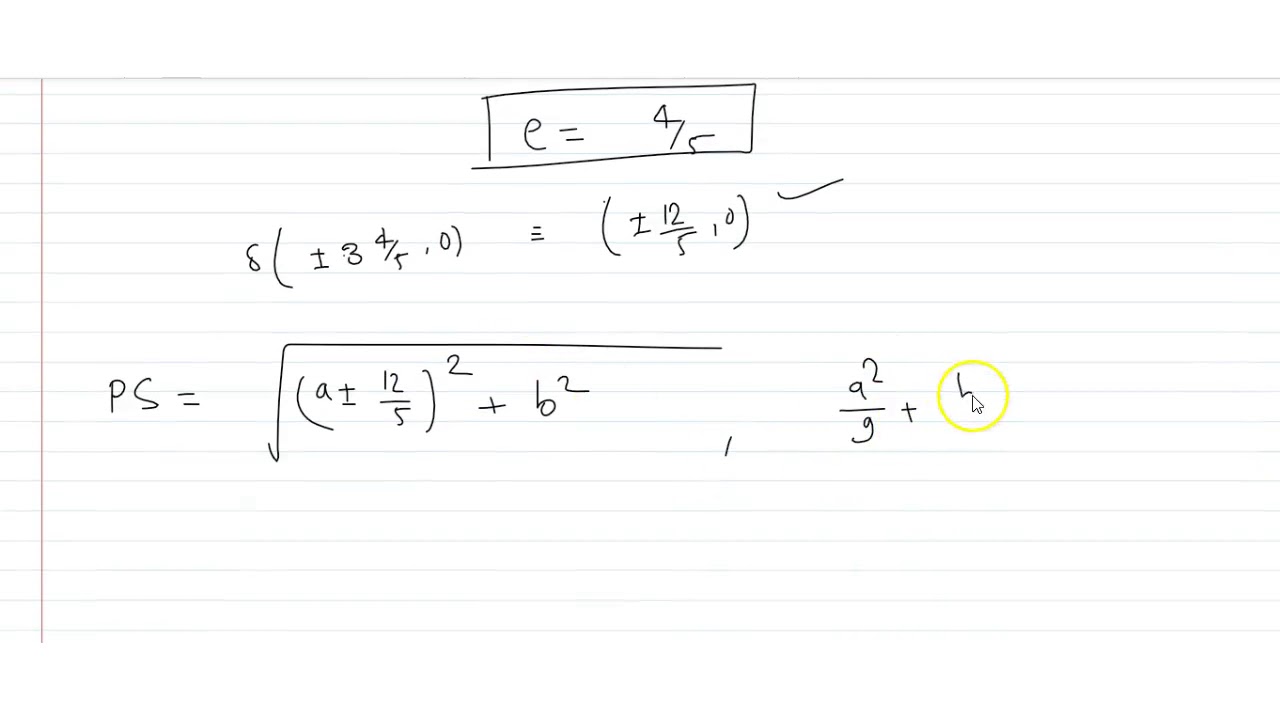



The Distance From The Foci Of P A B On The Ellipse X 2 9 Y 2 25 1 Are Youtube




Hyperbolas
Click here👆to get an answer to your question ️ The eccentric angle of the point where the line, 5x 3y = 8√(2) is a normal to the ellipse x^2/25 y^2/9 = 1 isYour approach would have been correct if the point lied outside the ellipse but since it lies inside the ellipse your method only calculates the square of one part of the chord on which the point lies because since an ellipse is symmetrical you can draw two equal chords through a pointTo solve this correctly remember that the diameter of a ellipse through a point is largest among all chords Find the coordinate of the vertices foci eccentricity and length of latus rectum of the hyperbola x^2/25y^2/4 =1 asked Jan in Coordinate



The Smaller Region Bounded By The Ellipse X 2 16 Y 2 9 1 And A Straight Line 3x 4y 12 What Should Be The Area Of That Smaller Region Quora
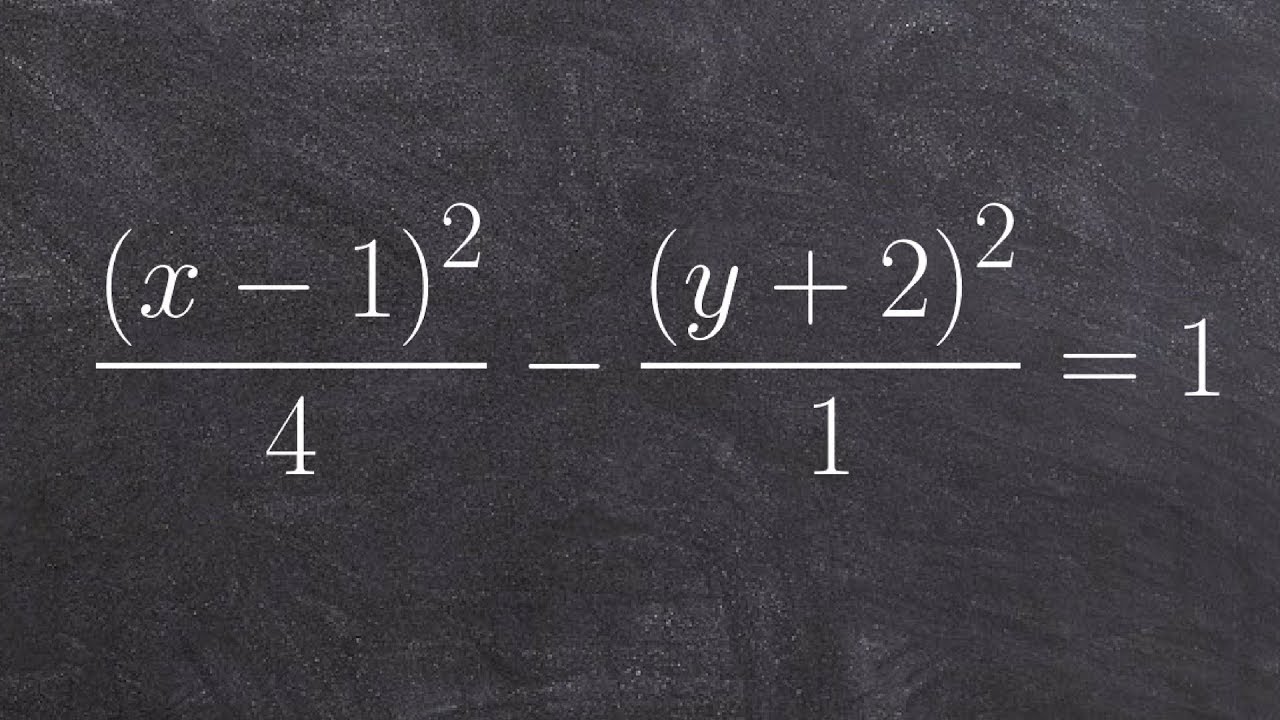



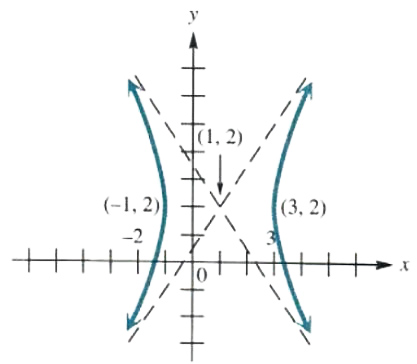
Finding The Vertices Foci And Asymptotes Of A Hyperbola Youtube
Math 116 HWK 8b Solns continued §62 p463 Problem 29, §62, p 463 Find the volume of the solid S, given that the base of S is an elliptical region with boundary curve 9x 24y = 36 and crosssections perpendicular to the xaxis are isosceles right triangles with hypotenuse in the baseSOLUTION What are the coordinates of the endpoints of the major axis in the graph of x^2/25 y^2/9=1 Algebra > Quadraticrelationsandconicsections> SOLUTION What are the coordinates of the endpoints of the major axis in the graph of x^2/25 y^2/9=1 Log On Algebra Conic sections ellipse, parabola, hyperbola SectionHomework Solutions MATH 32B2 (18W) Problem 10 () Sketch the region Dbetween y= x2 and y= x(1 x) Express Das a simple region and calculate the integral of f(x;y) = 2yover D




The Ellipse With Foci At 3 0 And 3 0 And Chegg Com



Solve Ellipse And Hyperbola Step By Step Math Problem Solver
Compare and contrast the graphs of the equations x 2 4 y 2 9 = 1 x 2 4 y 2 9 = 1 and x 2 9 y 2 4 = 1 x 2 9 y 2 4 = 1 146 Explain in your own words, the difference between a vertex and aCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history Example 14 Find the coordinates of the foci and the vertices, the eccentricity, the length of the latus rectum of the hyperbolas (i) x2/9 − y2/16 = 1, The given equation is 𝑥2/9 − 𝑦2/16 = 1 The above equation is of the form 𝑥2/𝑎2 − 𝑦2/𝑏2 = 1 Comparing (1) & (2) a2 = 9 a




Ex 11 3 4 X2 25 Y2 100 1 Find Foci Latus Rectum Ex 11 3




The Length Of The Latus Rectum Of The Ellipse X 2 25 Y
1) or equivalently x ′ = x − h {\displaystyle x'=xh} and y ′ = y − k {\displaystyle y'=yk} (2) In the new coordinate system, the point P will appear to have been translated in the opposite direction For example, if the xy system is translated a distance h to the right and a distance k upward, then P will appear to have been translated a distance h to the left and a distance kX^2/25y^2/9=1 vertices (x,y) = ( ) (smaller xvalue) (x, y) = ( ) (larger xvalue) foci (x,y) = ( ) (smaller xvalue) (x, y) = ( ) (larger xvalue) Sketch its graph Expert Answer 100% (2 ratings) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculatorExpand Factor x^ {2}25 Factor x^ {2}2x15 Factor x 2 − 2 5 Factor x 2 − 2 x − 1 5 To add or subtract expressions, expand them to make their denominators the same Least common multiple of \left (x5\right)\left (x5\right) and \left (x5\right)\left (x3\right) is \left (x5\right)\left (x3\right)\left (x5\right) Multiply \frac
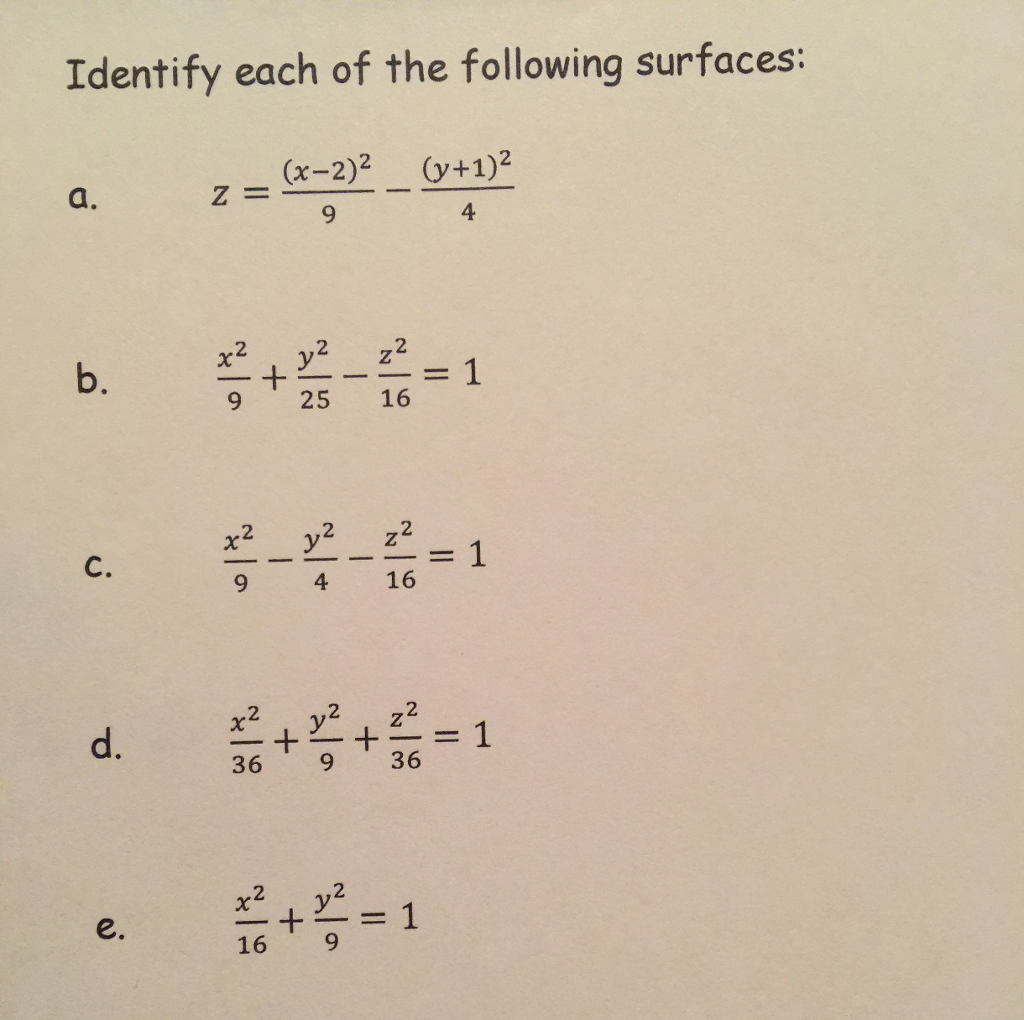



Identify Each Of The Following Surfaces Z X Chegg Com




Ex 11 4 1 Find Foci Vertices Of Hyperbola X 2 16 Y 2 9 1
Here, P, Q, R and S are the conormal points (i) The sum of the eccentric angles of the conormal points on the ellipse, x 2 / a 2 y 2 / b 2 = 1 is an odd multiple of π (ii) If θ 1, θ 2, θ 3 and θ 4 are eccentric angles of four points on the ellipse, the normals at which are concurrent, then (a) Σ cos (θ 1 θ 2) = 0 (b) Σ sin (θ 1 θ 2) = 0 (iii) If θ 1, θ 2 and θ 3 are theCalculadoras gratuitas passo a passo para álgebra, trigonometria e cálculoFind the center, transverse axis, vertices, foci, and asymptotes for the hyperbola
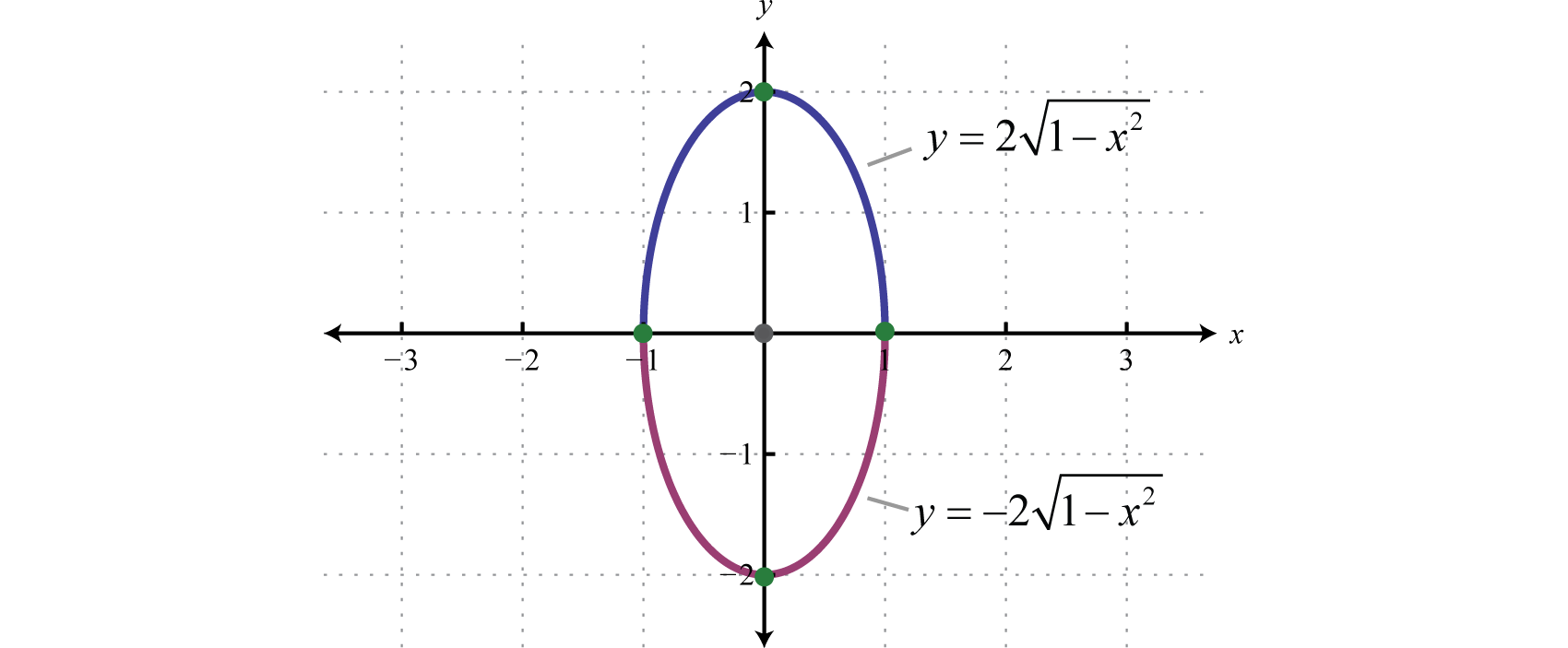



Ellipses
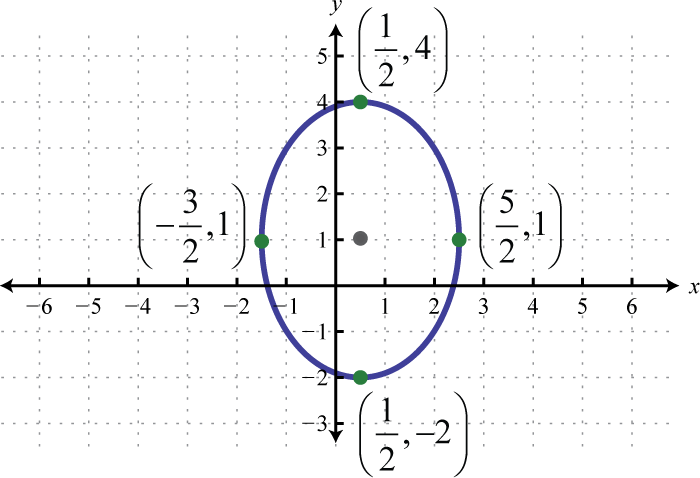



Ellipses
(Enter them as commaseparated orderedpairs, eg, (1,3), (2,5) Enter none if there are no such points) slope is undefined at____ Please helpThe Curves Can Be Modeled Be The Equation ((x^2)/25)((y^2/9))=1, Where The Units Are In Meters?




The Foci Of A Hyperbola Coincide With The Foci Of The Ellipse X 2 25 Y 2 9 1 If The Youtube
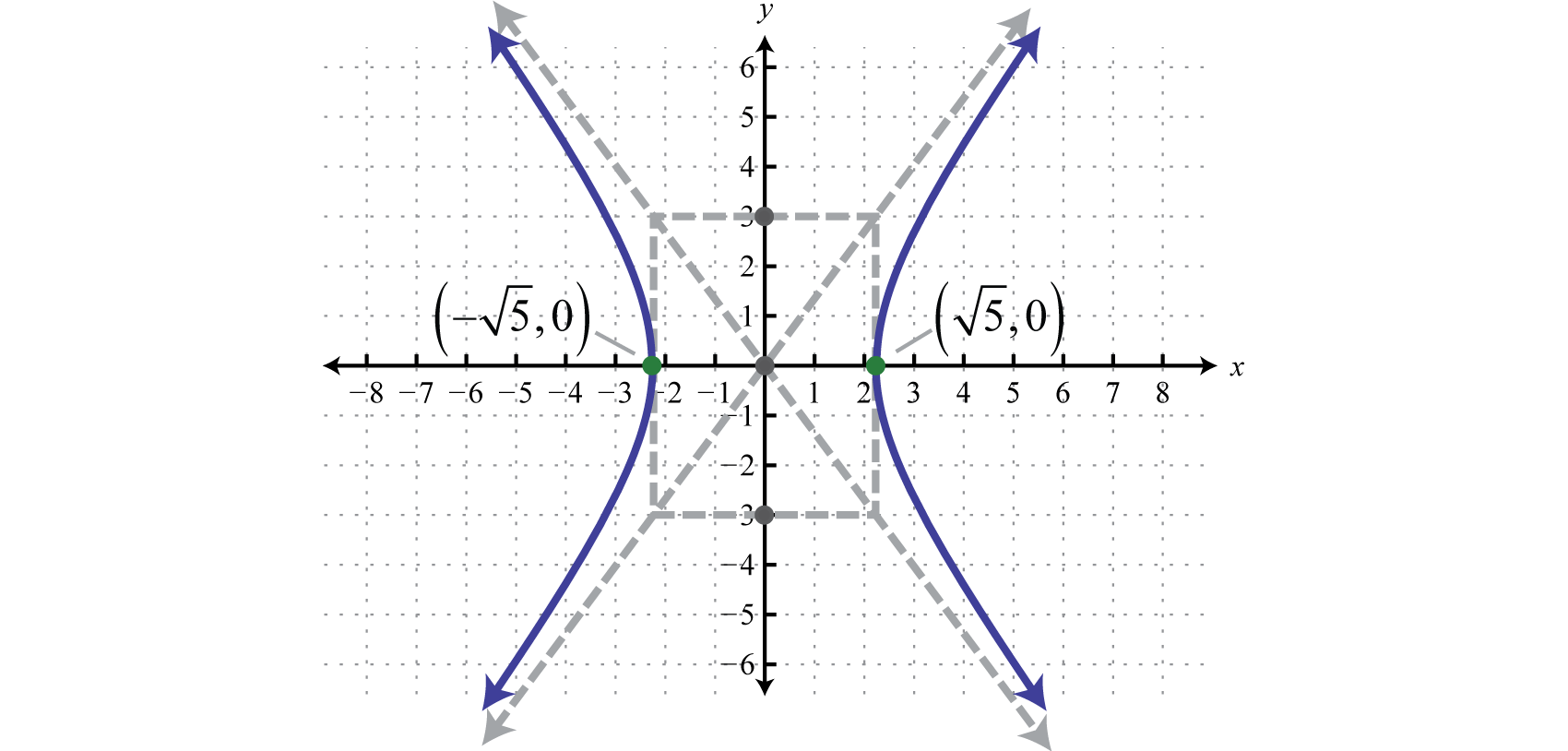



8 4 Hyperbolas Mathematics Libretexts
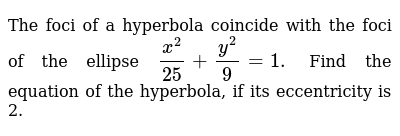



The Foci Of A Hyperbola Coincide With The Foci Of The Ellipse
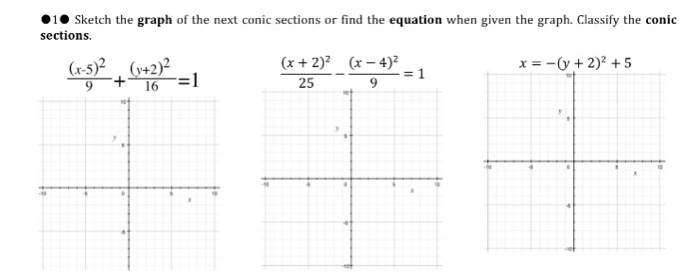



Solved Sketch The Graph Of The Next Conic Sections Or Fin Chegg Com




Consider An Ellipse X 2 25 Y 2 9 1 With Centre C And A Point P




7 03 Ellipses And Circles




Consider An Ellipse X 2 25 Y 2 9 1 With Centre C And A Point P On It With Eccentric Angle Youtube



Solution How To Graph X 2 25 Y 2 9 1




The Eccentricity Of The Hyperbola X 2 25 Y 2 16 1 Is



The Area Of The Region Bounded By The Ellipse X2 25 Y2 16 1 Is Studyrankersonline




Los Vertices Mayores De La Elipse X 2 25 Y 2 9 1 Son Seleccione Una A 5 5 Y 10 5 B 0 5 Brainly Lat




Section 11 6 Conic Sections Ppt Download




The Focii X 2 25 Y 2 9 1 Coincide With The Hyperbola It



Hyperbola X 2 25 Y 2 9 1 Youtube



Ellipses




Conic Sections



Ellipses And Hyperbolae
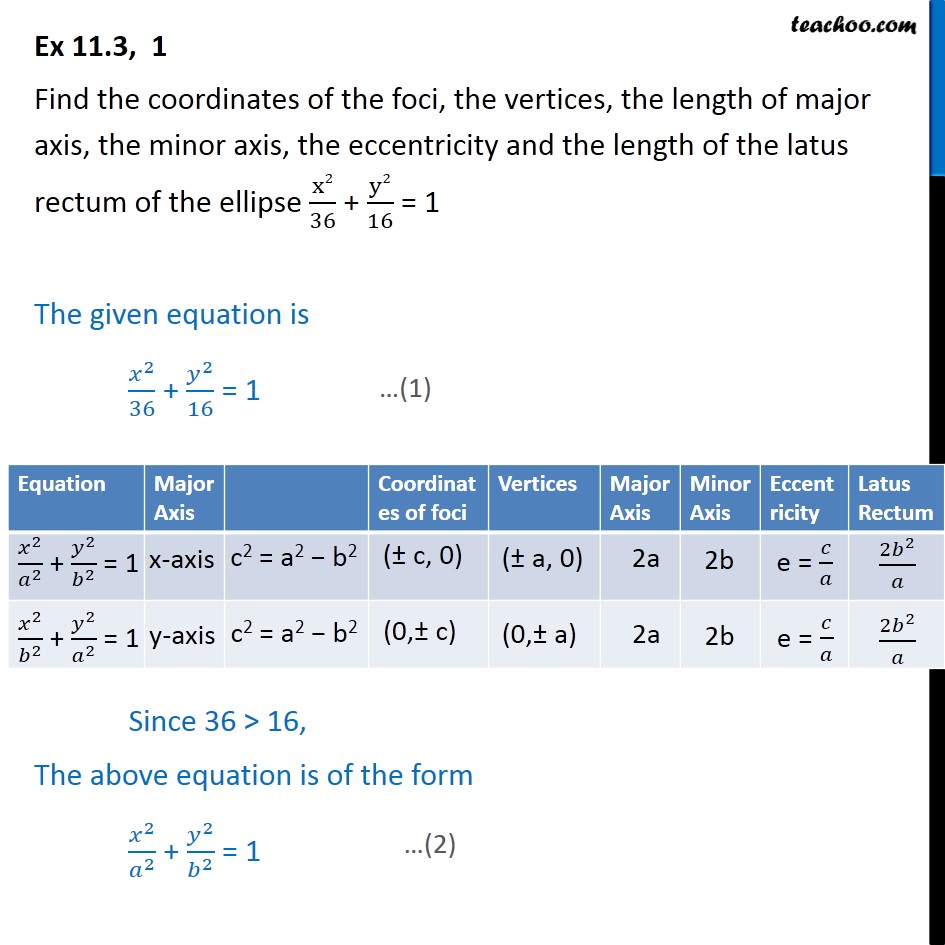



Ex 11 3 1 X2 36 Y2 16 1 Find Foci Vertices Eccentricity
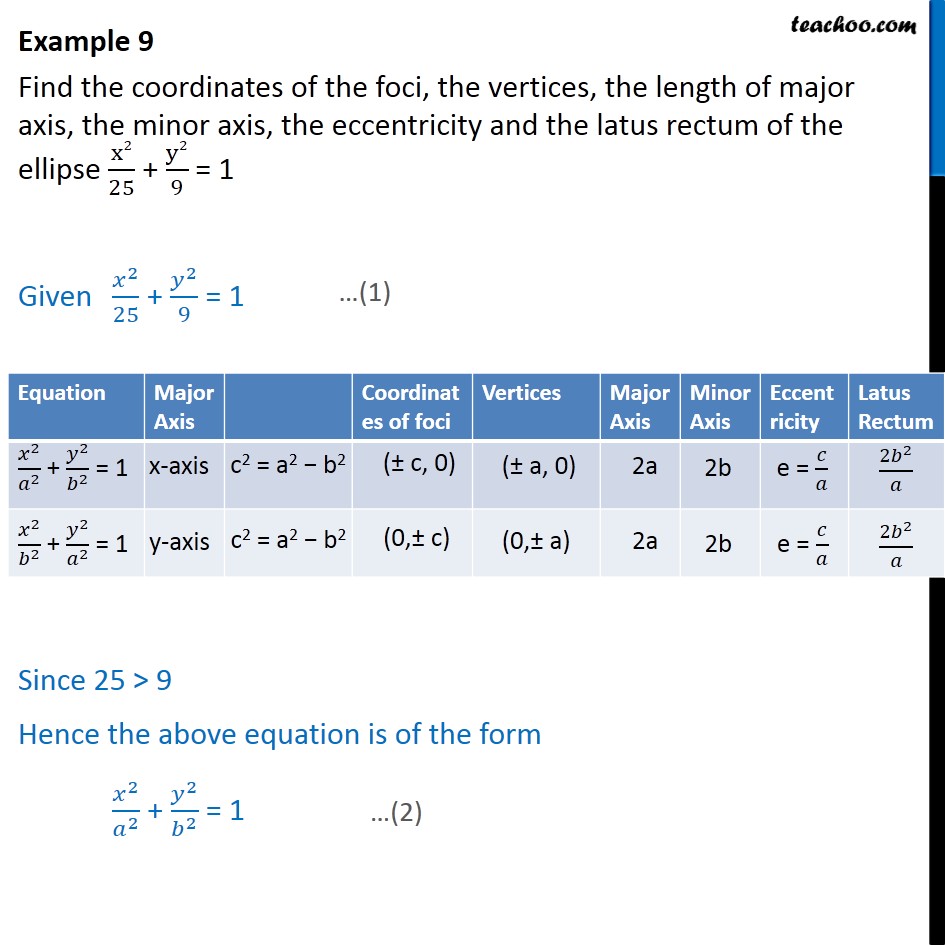



Example 9 X2 25 Y2 9 1 Find Foci Vertices Eccentricity




Hyperbolas




Solved Find The Equation Of The Hyperbola With Vertices Chegg Com



Solution Hello Again Double Checking An Answer This Is The Equation Of A Horizontal Hyperbola X 1 2 25 Y 3 2 9 1 A True B False I Think It 39 S False I 39 M Making Sure Though



15 6 Surface Integrals Chapter 15 Vector Analysis Part Calculus Iii




Find The Standard Form Of The Equation Of The Ellipse Chegg Com
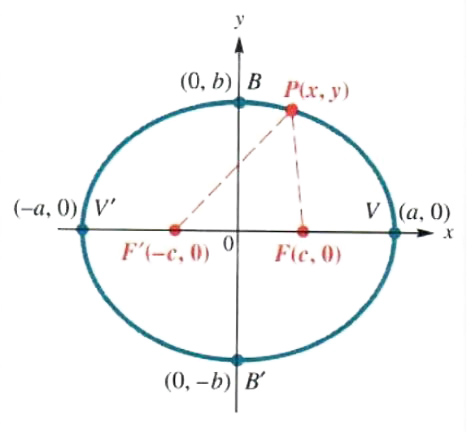



Solve Ellipse And Hyperbola Step By Step Math Problem Solver



What Is The Center Of The Ellipse Math Frac X Y 2 2 9 Frac X Y 2 16 1 Math Quora




Vertices Direction Of A Hyperbola Example 2 Video Khan Academy



Hyperbola3 Html



Solved The Top Of The Ellipses Is The Point 0 Y2 Ellips Chegg Com




Ex 8 1 4 Find Area Bounded By Ellipse X2 16 Y2 9 1




Find The Eccentricity Each Of The Following Ellipses Frac X 2 25 Frac Y 2 9 1 Snapsolve



How To Construct The Graph Of X 2 Y 2 9 Quora



Solution Find The Vertices And Foci Of The Hyperbola Draw The Graph Y 2 25 X 2 21 1 X 2 9 Y 2 16 1



12 6 Quadric Surfaces Mathematics Libretexts



1




Wbjee Math Questions And Answers Helpyout




Example 9 X2 25 Y2 9 1 Find Foci Vertices Eccentricity
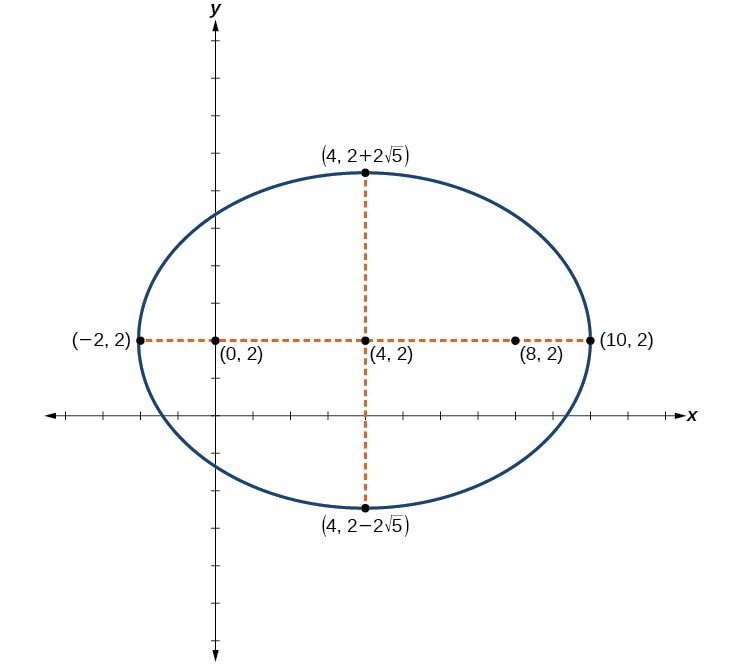



Graphs Of Ellipses College Algebra



The Smaller Region Bounded By The Ellipse X 2 16 Y 2 9 1 And A Straight Line 3x 4y 12 What Should Be The Area Of That Smaller Region Quora
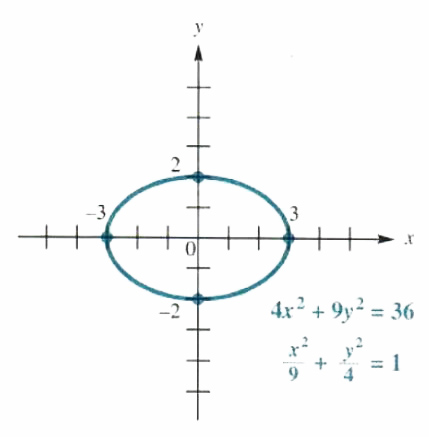



Solve Ellipse And Hyperbola Step By Step Math Problem Solver
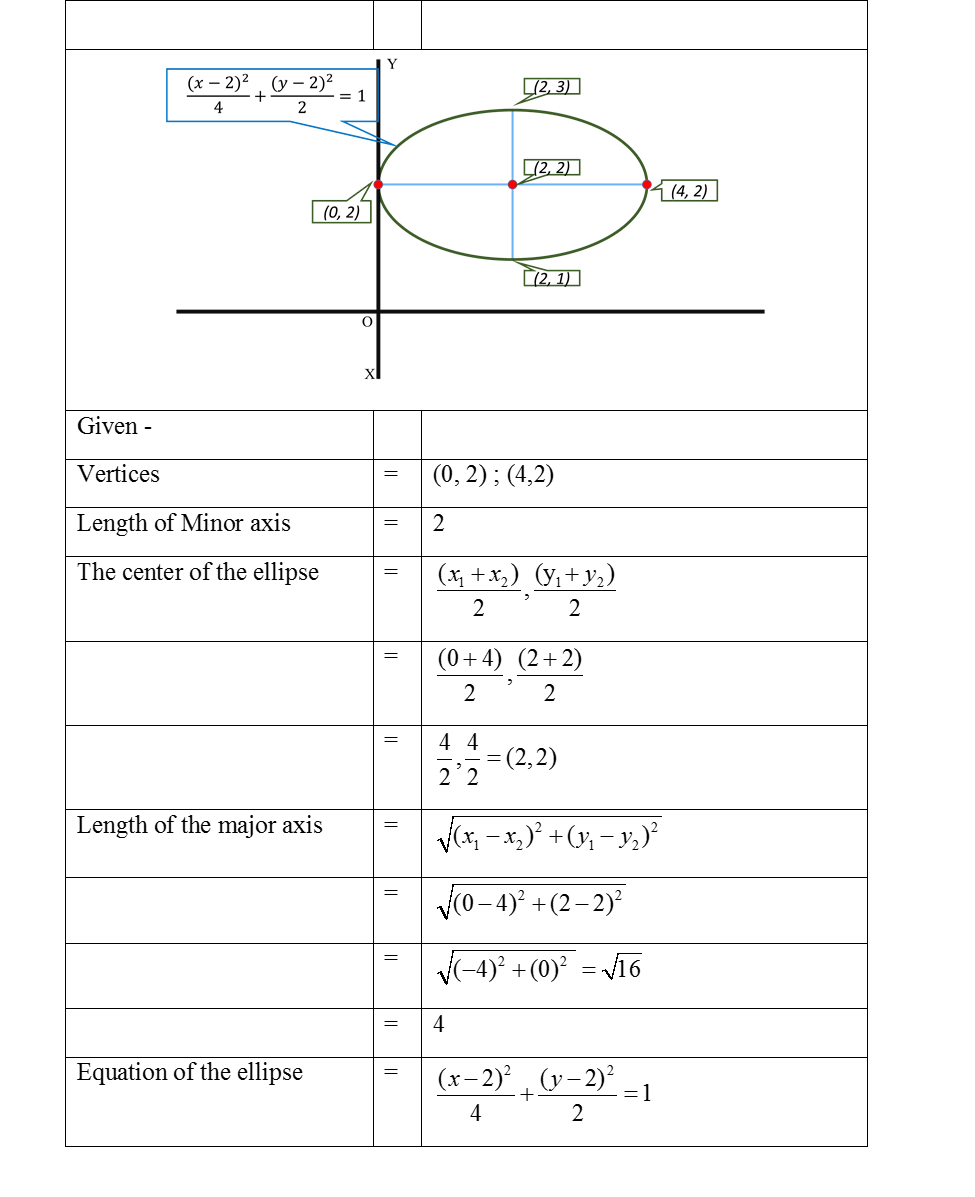



How Do You Write An Equation Of A Ellipse With Vertices 0 2 4 2 And Minor Axis Of Length 2 Socratic




Hyperbolas



The Area Of The Region Bounded By The Ellipse X 2 25 Y 2 16 1 Is Sarthaks Econnect Largest Online Education Community



Solved 2 The Equation Of The Red Ellipse In The Figure S Chegg Com



What Is The Center Of The Ellipse Math Frac X Y 2 2 9 Frac X Y 2 16 1 Math Quora
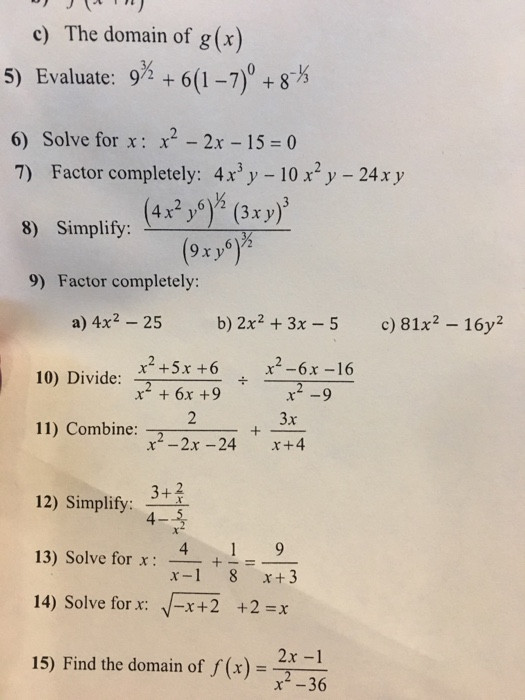



Evaluate 9 3 2 6 1 7 0 8 1 3 Solve For X Chegg Com




7 04 Hyperbolas




The Ellipsoid Shown At Right Has Equation X 2 9 Chegg Com
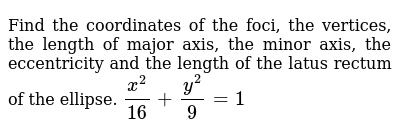



X 2 16 Y 2 25 1 The Length Of The Major Axis Is




Solved For The Equation Of An Ellipse Given Below State Chegg Com




Consider An Ellipse X 2 25 Y 2 9 1 With Centre C And A Point P
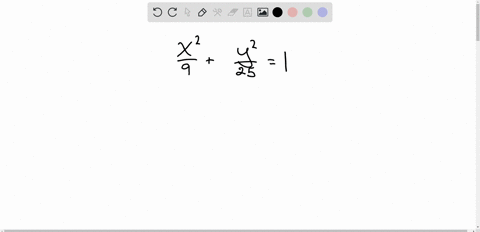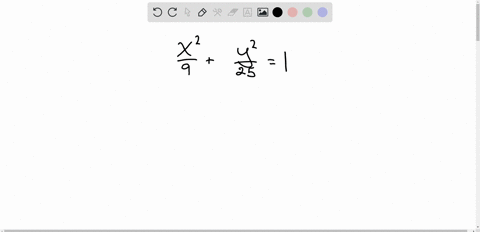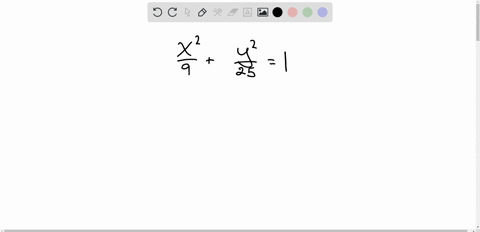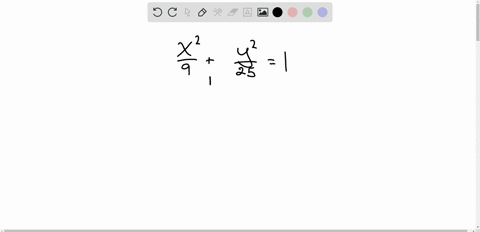



Solved Match Each Equation With The Correct Graph
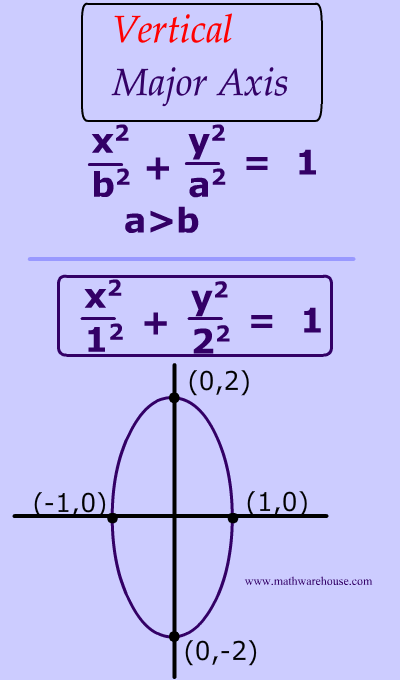



Equation Of An Ellipse In Standard Form And How It Relates To The Graph Of The Ellipse




The Angle Between The Curves X 2 25 Y 2 9 1 And X 2 8 Y 2 8



1



Http Www Math Utep Edu Faculty Cmmundy Math 2301 Solution Manual Pdf



Search Q Find The Area Of The Shaded Region Tbm Isch



Solution X 2 25 Y 2 9 1
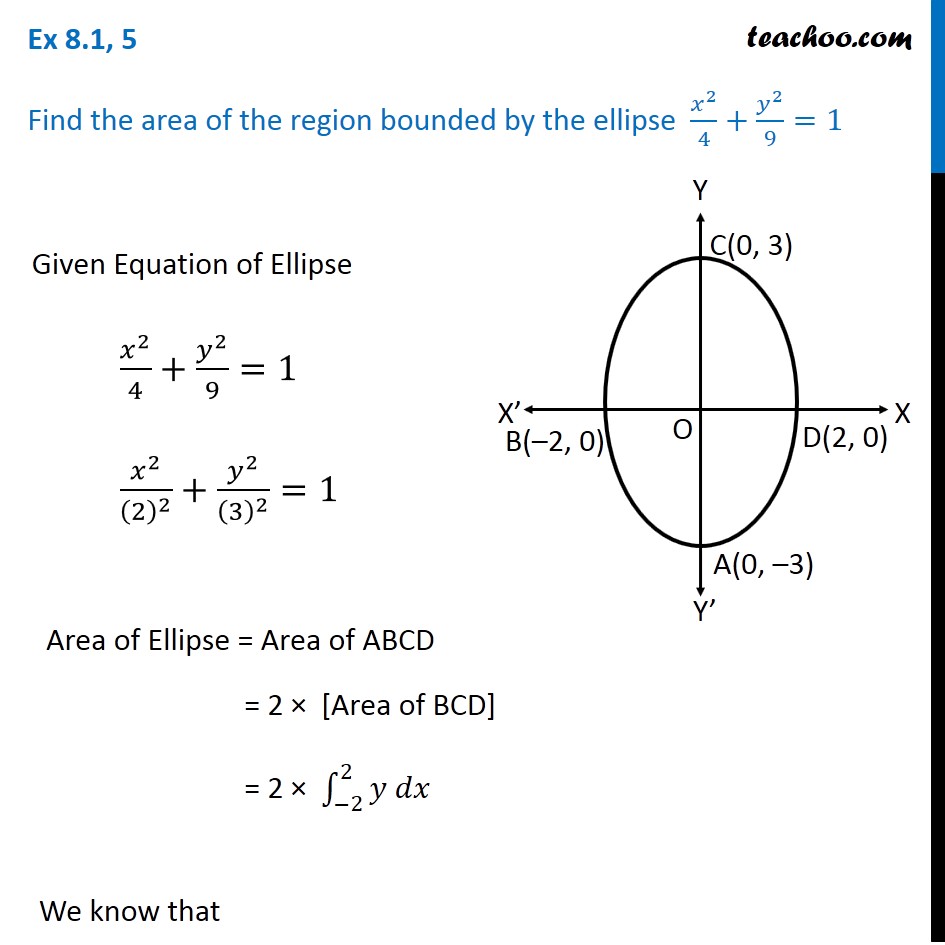



Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12




If A Hyperbola Passes Through The Foci Of The Ellipse X 2




The Length Of The Tangent Of The Ellipse X 2 25 Y 2 16 1 Interc




Match The Equation With Its Graph The Graphs Are Chegg Com
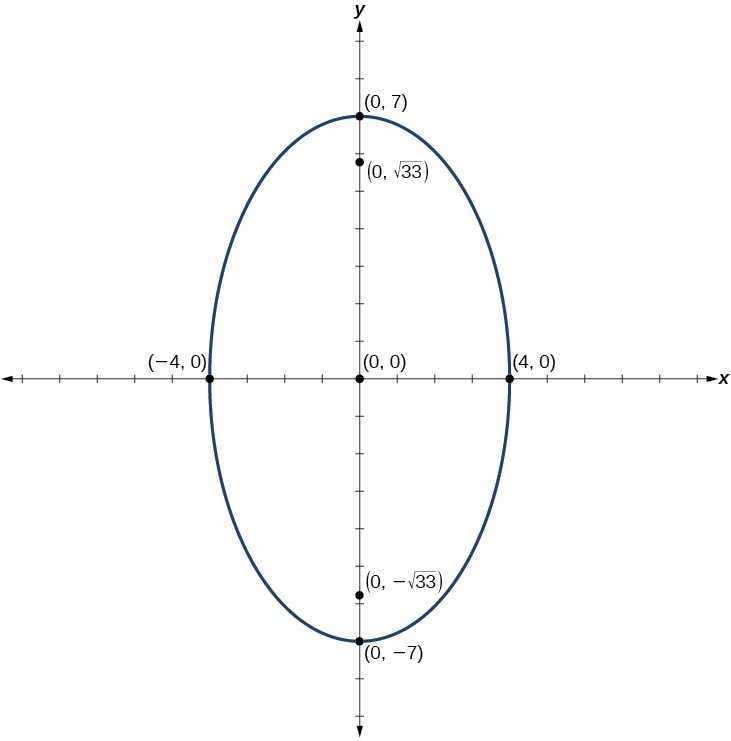



Graphs Of Ellipses College Algebra



Find Eccentricity Of The Hyperbola X 2 16 Y 2 9 1 Sarthaks Econnect Largest Online Education Community
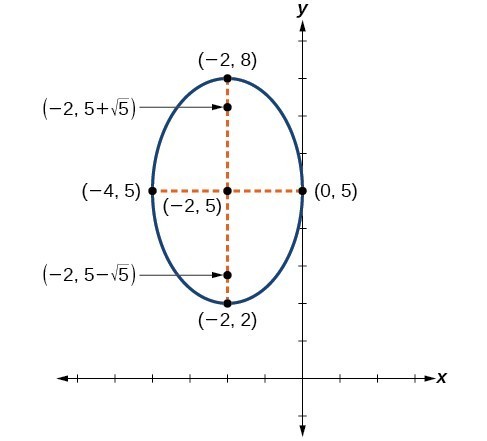



Graphs Of Ellipses College Algebra



The Foci Of A Hyperbola Coincide With The Foci Of The Ellipse X 2 25 Y 2 9 1 Find The Equation Of The Hyperbola Sarthaks Econnect Largest Online Education Community



Let E1 And E2 Be The Eccentricities Of The Ellipse X 2 25 Y 2 B 2 1 B 5 And The Hyperbola X 2 16 Y 2 B 2 1 Sarthaks Econnect Largest Online Education Community



Ellipses And Hyperbolae



Www Nrcs Net Downloads T7 2 hw odds and evens3 Pdf




Consider Any P On The Ellipse X 2 25 Y 2 9 1 In The First




Consider The Ellipsoid Given By The Equation X 2 1 Chegg Com




Equation Of A Circle
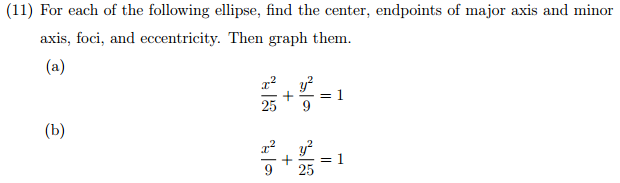



Solved For Each Of The Following Ellipse Find The Center Chegg Com




If The Foci Of The Ellipse X 2 16 Y 2 B 2 1 And The Hype




Solved Use The Center Vertices And Asymptotes To Graph Chegg Com
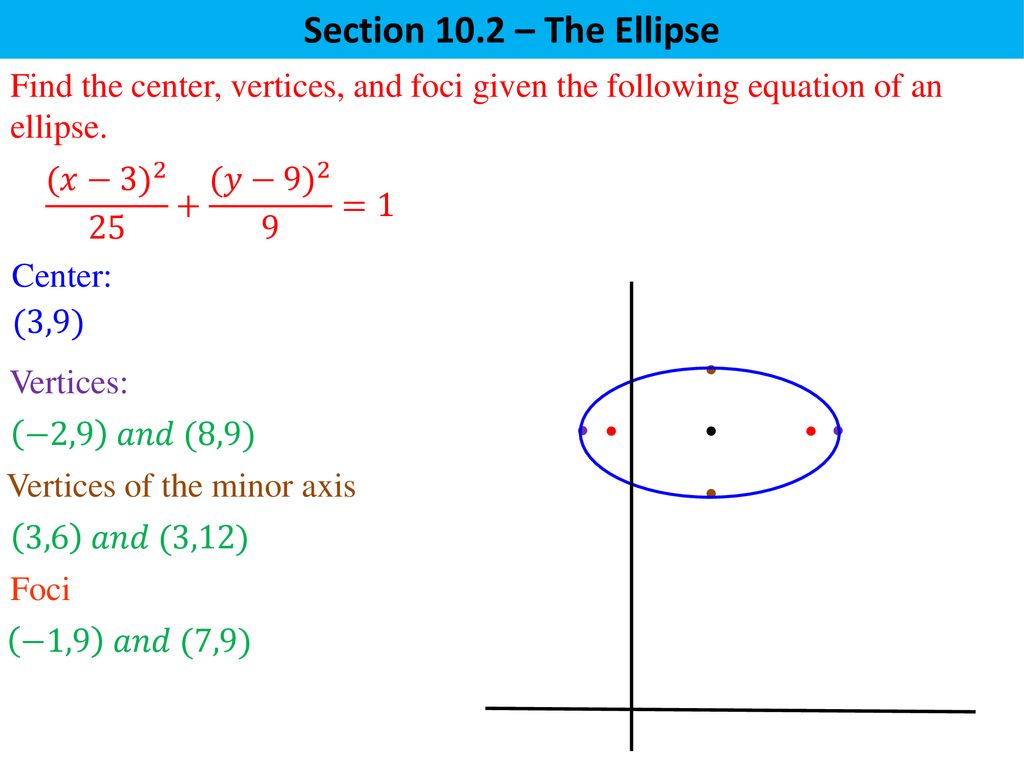



Section 10 2 The Ellipse Ellipse A Set Of Points In A Plane Whose Distances From Two Fixed Points Is A Constant Ppt Download


